已知焦点在x轴上的椭圆$\frac{x^2}{16}+\frac{y^2}{m}=1$的离心率为$\frac{1}{2}$.则m等于12．题目和参考答案——青夏教育精英家教网——

题目内容

14．已知焦点在x轴上的椭圆$\frac{x^2}{16}+\frac{y^2}{m}=1$的离心率为$\frac{1}{2}$，则m等于12．

分析由题意可得a=4，b=$\sqrt{m}$，c=$\sqrt{16-m}$，又e=$\frac{c}{a}$，解方程即可得到所求值．

解答解：由题意可得a=4，b=$\sqrt{m}$，c=$\sqrt{16-m}$，
又e=$\frac{c}{a}$=$\frac{\sqrt{16-m}}{4}$=$\frac{1}{2}$，
解得m=12．
故答案为：12．

点评本题考查椭圆的离心率公式的运用，考查运算能力，属于基础题．

练习册系列答案

全优期末真题8套系列答案

期末好卷系列答案

红领巾乐园系列答案

初中英语最佳方案冲刺AB卷系列答案

新中考指南系列答案

快乐起跑线期末冲刺系列答案

快乐起跑线周考卷系列答案

快乐起跑线单元滚动活页测系列答案

快乐学习一点通系列答案

智慧翔课时导学案系列答案

相关题目

16．已知数列{C_n}，其中C_n=2ⁿ+3ⁿ．
（1）数列{C_n}是否为等比数列？证明你的结论；
（2）若{C_n+1-pC_n}为等比数列，求实数p．

5．已知椭圆C₂过椭圆C₁：$\frac{{x}^{2}}{14}+\frac{{y}^{2}}{9}=1$的两个焦点和短轴的两个端点，则椭圆C₂的离心率为（　　）

$\frac{\sqrt{2}}{2}$

2．已知函数f（x）的导函数f′（x）=a（x-1）（x-a），若f（x）在x=a处取得极大值，则实数a的取值范围是（0，1）．

9．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{2}}{2}$，且短轴长为6．
（Ⅰ）求椭圆的标准方程；
（Ⅱ）是否存在斜率为1的直线l，使得l与曲线C相交于A，B两点，且以AB为直角的圆恰好经过原点？若存在，求出直线l的方程；若不存在，请说明理由．

19．已知椭圆C₁：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为e=$\frac{\sqrt{3}}{2}$，且C₁的右焦点与抛物线C₂：y²=4$\sqrt{3}$x的焦点相同．
（1）求椭圆C1的方程；
（2）求经过点P（-2，0）分别作斜率为k₁、k₂（k₁≠k₂）的两条直线，两直线分别与椭圆C₁交于M、N两点，当直线MN与y轴垂直时，求k₁•k₂的值．

6．已知函数f（x）=e^x-ax在（3，+∞）单调递增，则实数a的取值范围是（-∞，e³]．

3．某几何体的三视图如图所示，则其表面积为（　　）

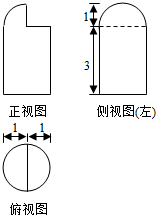
$\frac{17π}{2}$

$\frac{19π}{2}$

4．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的离心率为$\frac{\sqrt{6}}{3}$，右焦点为（$\sqrt{2}$，0）．
（1）求椭圆C的方程；
（2）若过原点O作两条互相垂直的射线，与椭圆交于A，B两点，求证：点O到直线AB的距离为定值；
（3）在（2）的条件下，求△OAB面积的最大值．