题目内容
6.有编号为1,2,3,4,5的五个小球和编号为1,2,3,4的四个盒子,现把球全部放入盒子中,(1)若恰有一个盒子不放球,有多少种放法?
(2)若每个盒子都不空,恰有两个小球放入编号相同的盒子,有多少种放法?
(3)若每个盒子都不空,且编号为偶数的小球只放入编号为偶数的盒子中,有多少种放法?
分析 (1)分三个盒子中球的个数为“122型”或“113型”两种情况讨论即可;
(2)利用捆绑法计算即得结论;
(3)分2号球入2号盒、4号球入4号盒,2号球入4号盒、4号球入2号盒两种情况讨论即可.
解答 解:(1)依题意,三个盒子中球的个数为“122型”或“113型”,
①若为“122型”时,此时有${C}_{3}^{1}$•${A}_{5}^{3}$•${C}_{3}^{2}$•${A}_{2}^{2}$=360种放法;
②若为“112型”时,此时有${C}_{3}^{1}$•${A}_{5}^{3}$•${C}_{3}^{1}$=180种放法;
综上所述,若恰有一个盒子不放球,有360+180=540种放法;
(2)将放入编号相同盒子的两球看做一个小球,则相当于将4个小球放入4个不同的盒子,
故有${C}_{5}^{2}$•${A}_{4}^{4}$=240种放法;
(3)∵每个盒子都不空,
∴恰有一个盒子有2个球,其他的盒子均有一个球,
依题意,分以下情况讨论:
①当2号球入2号盒时,则4号球必入4号盒,
此时有${A}_{3}^{2}$•${C}_{2}^{1}$=12种放法;
②当2号球入4号盒时,则4号球必入2号盒,
此时有${A}_{3}^{2}$•${C}_{2}^{1}$=12种放法;
综上所述,有12+12=24种放法.
点评 本题考查排列、组合及简单计数问题,考查分类讨论的思想,注意解题方法的积累,属于中档题.

练习册系列答案
 浙大优学小学年级衔接捷径浙江大学出版社系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
1.抛掷一枚骰子,事件M:向上的点数是1,3,5,事件N:向上的点数是奇数,则下列不成立的是( )
| A. | M=N | B. | M⊆N | C. | N⊆M | D. | N>M |
11.已知三棱锥P-ABC,在底面△ABC中,∠A=60°,BC=$\sqrt{3}$,PA⊥面ABC,PA=2$\sqrt{3}$,则此三棱锥的外接球的表面积为( )
| A. | $\frac{16}{3}$π | B. | 4$\sqrt{3}$π | C. | $\frac{32}{3}$π | D. | 16π |
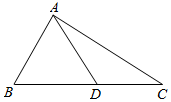 如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.
如图,在△ABC中,B=$\frac{π}{3}$,AC=$\sqrt{3}$,D为BC边上一点.若AB=AD,则△ADC的周长的取值范围为.