题目内容
已知(3x-1)n的展开式的奇数项二项式系数和是16,求(x
-3x2)n的展开式中:
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
| 2 |
| 3 |
(1)二项式系数最大的项;
(2)系数的绝对值最大的项.
考点:二项式系数的性质
专题:二项式定理
分析:(1)先由条件求得n=5,可得二项式系数最大的项为第三、四两项,利用通项公式求得这两项.
(2)设展开式中第r+1项系数的绝对值最大,则由Tr+1=(-3)r•
•x
,可得
,由此求得自然数r的值.
(2)设展开式中第r+1项系数的绝对值最大,则由Tr+1=(-3)r•
| C | r 5 |
| 10+4r |
| 3 |
|
解答:
解:由题意可得 2n-1=16,解得n=5.
(1)∵n=5,展开式共6项,二项式系数最大的项为第三、四两项,
∴T3=
2•( x
)3•(3x2)2=90x6,T4=
(x
)2(-3x2)3=-270x
.
(2)设展开式中第r+1项系数的绝对值最大,
则Tr+1=(-3)r•
•x
,根据
求得
≤r≤
,
求得r=4.
即展开式中第5项系数的绝对值最大,即T5=
(x
)(-3x2)4=405x
.
(1)∵n=5,展开式共6项,二项式系数最大的项为第三、四两项,
∴T3=
| C | 5 |
| 2 |
| 3 |
| C | 3 5 |
| 2 |
| 3 |
| 22 |
| 3 |
(2)设展开式中第r+1项系数的绝对值最大,
则Tr+1=(-3)r•
| C | r 5 |
| 10+4r |
| 3 |
|
| 7 |
| 2 |
| 9 |
| 2 |
求得r=4.
即展开式中第5项系数的绝对值最大,即T5=
| C | 4 5 |
| 2 |
| 3 |
| 26 |
| 3 |
点评:本题主要考查二项式定理的应用,二项展开式的通项公式,求展开式中某项的系数,二项式系数的性质,属于中档题.

练习册系列答案
 全能练考卷系列答案
全能练考卷系列答案
相关题目
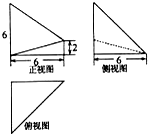
若某空间几何体的三视图如图所示,则该几何体的体积是( )

| A、16 | B、32 | C、48 | D、144 |
已知A={x|y=
},B={y|y=log2(x2+4)},则A∩B=( )
| 3-|x-2| |
| A、∅ | B、[2,5] |
| C、[-1,5] | D、[2,+∞] |
