题目内容
在△ABC中，A：B：C=2：0.5：0.5，则a：b：c=（ ）
| A、2：0.5：0.5 | ||
B、
| ||
C、
| ||
| D、120：30：30 |
考点：正弦定理
专题：解三角形
分析：根据角之间的关系求出A，B，C的大小，利用正弦定理即可求出边之间的关系．
解答：
解：∵，A：B：C=2：0.5：0.5，
∴，A=120°，B=C=30°，
∴根据正弦定理可知a：b：c=sinA：sinB：sinC=sin120°：sin30°：sin30°=
：
：
=
：1：1，
故选：C．
∴，A=120°，B=C=30°，
∴根据正弦定理可知a：b：c=sinA：sinB：sinC=sin120°：sin30°：sin30°=
| ||
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 3 |
故选：C．
点评：本题主要考查正弦定理的应用，根据条件求出A，B，C的大小是解决本题的关键．
练习册系列答案
世纪百通期末金卷系列答案
相关题目
已知A={x|f（x）=lg（x2-x-2），x∈R}，B={x||x+1|＜4，x＞0}，则A∩B=（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
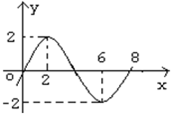函数f（x）=Asin（ωx+ϕ）（A＞0，ω＞0）的部分图象如图所示，则f（1）+f（2）+…+f（11）的值是（ ）A、2+2
| ||
B、2-2
| ||
| C、0 | ||
| D、-1 |