题目内容
已知a∈R，设P：函数y=ax在R上递增，Q：关于x的不等式ax2-ax+1＞0对?x∈R恒成立．如果P且Q为假，P或Q为真，求a的取值范围．
考点：复合命题的真假
专题：常规题型,简易逻辑
分析：P且Q为假，P或Q为真，则P、Q一真一假．
解答：
解：由函数y=ax在R上递增为真可得，a＞1；
由关于x的不等式ax2-ax+1＞0对?x∈R恒成立可得，0≤a＜4．
∵P且Q为假，P或Q为真，
∴①P真Q假时，a≥4；
②P假Q真时，0≤a≤1；
则a的取值范围为[0，1]∪[4，+∞）．
由关于x的不等式ax2-ax+1＞0对?x∈R恒成立可得，0≤a＜4．
∵P且Q为假，P或Q为真，
∴①P真Q假时，a≥4；
②P假Q真时，0≤a≤1；
则a的取值范围为[0，1]∪[4，+∞）．
点评：本题考查了复合命题的真假，属于基础题．
练习册系列答案
相关题目
已知单位向量
，
的夹角为
，则|
-4
|等于（ ）
| a |
| b |
| π |
| 3 |
| a |
| b |
| A、13 | ||
| B、11 | ||
C、
| ||
D、
|
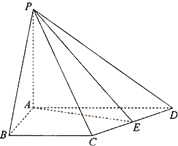如图所示，在四棱锥P-ABCD中，PA⊥平面ABCD，AB=4，BC=3，AD=5，∠DAB=∠ABC=90°，E是D的中点．证明：CD⊥平面PAE．