题目内容
(1)计算:
lg25+lg2-lg
-log29×log32;
(2)化简:
.
| 1 |
| 2 |
| 0.1 |
(2)化简:
| cos(-α-π)•sin(2π+α) |
| cos(-α)•tanα |
考点:同角三角函数基本关系的运用,运用诱导公式化简求值
专题:三角函数的求值
分析:(1)原式利用对数的运算法则变形,计算即可得到结果;
(2)原式利用诱导公式化简,计算即可得到结果.
(2)原式利用诱导公式化简,计算即可得到结果.
解答:
解:(1)原式=lg5+lg2+
lg10-2log23×log32=1+
-2=-
;
(2)原式=
=-cosα.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
(2)原式=
| -cosα•sinα | ||
cosα•
|
点评:此题考查了同角三角函数基本关系的运用,熟练掌握基本关系是解本题的关键.

练习册系列答案
相关题目
半径为3cm,中心角为
的弧长为( )
| 2π |
| 3 |
A、
| ||
| B、πcm | ||
C、
| ||
| D、2πcm |
复数(1-2i)2的虚部为( )
| A、-4 | B、-2 | C、2 | D、2i |
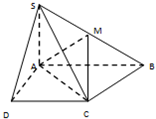 如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
如图已知四棱锥S-ABCD的底面是直角梯形,AB∥DC,∠DAB=90°,SA⊥底面ABCD,且SA=AD=DC=
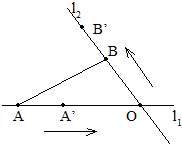 为进行科学实验,观测小球A、B在两条相交成60°角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道l1、l2按箭头的方向运动.问:
为进行科学实验,观测小球A、B在两条相交成60°角的直线型轨道上运动的情况,如图所示,运动开始前,A和B分别距O点3m和1m,后来它们同时以每分钟4m的速度各沿轨道l1、l2按箭头的方向运动.问: