题目内容
19.过点M($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)作圆x2+y2=1的切线l,l与x轴的交点为抛物线E:y2=2px(p>0)的焦点,l与抛物线E交于A、B两点,则AB中点到抛物线E的准线的距离为( )| A. | $\frac{5\sqrt{2}}{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{7}{2}$$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
分析 利用已知条件求出切线方程,求出抛物线的焦点坐标,得到抛物线方程,联立直线与抛物线方程,利用韦达定理求出中点的横坐标,然后求解结果.
解答 解:过点M($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)作圆x2+y2=1的切线l,点在圆上,可得曲线的斜率为:1,
切线方程为:y+$\frac{\sqrt{2}}{2}$=x-$\frac{\sqrt{2}}{2}$,可得x-y-$\sqrt{2}$=0,直线与x轴的交点坐标($\sqrt{2}$,0),
可得抛物线方程为:y2=4$\sqrt{2}$x,
$\left\{\begin{array}{l}{{y}^{2}=4\sqrt{2}x}\\{y=x-\sqrt{2}}\end{array}\right.$,可得x2-6$\sqrt{2}x$+2=0,l与抛物线E交于A(x1,y1)、B(x2,y2),
可得:x1+x2=6$\sqrt{2}$,
则AB中点到抛物线E的准线的距离为:3$\sqrt{2}+\sqrt{2}$=4$\sqrt{2}$.
故选:D.
点评 本题考查抛物线的简单性质的应用,直线与抛物线的位置关系,考查计算能力.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
14.如果圆(x-a)2+(y-a)2=8上存在一点P到直线y=-x的最短距离为$\sqrt{2}$,则实数a的值为( )
| A. | -3 | B. | 3 | C. | $3\sqrt{2}$ | D. | -3或3 |
11.已知双曲线E:$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=6,P是E右支上一点,PF1与y轴交于点A,△PAF2的内切圆在边AF2上的切点为Q,若|AQ|=$\sqrt{3}$,则E的离心率是( )
| A. | 2$\sqrt{3}$ | B. | $\sqrt{5}$ | C. | $\sqrt{3}$ | D. | $\sqrt{2}$ |
8.已知某次数学考试的成绩服从正态分布N(116,82),则成绩在140分以上的考生所占的百分比为( )
(附:正态总体在三个特殊区间内取值的概率值①P(μ-σ<X≤μ+σ)=0.6826;②P(μ-2σ<X≤μ+2σ)=0.9544;③P(μ-3σ<X≤μ+3σ)=0.9974)
(附:正态总体在三个特殊区间内取值的概率值①P(μ-σ<X≤μ+σ)=0.6826;②P(μ-2σ<X≤μ+2σ)=0.9544;③P(μ-3σ<X≤μ+3σ)=0.9974)
| A. | 0.3% | B. | 0.23% | C. | 1.3% | D. | 0.13% |
9.已知函数f(x)=$\left\{\begin{array}{l}{lo{g}_{a}(2-x),x≤1}\\{|x-5|-1,3≤x≤7}\end{array}\right.$(a>0,且a≠1)的图象上关于直线x=1对称的点有且仅有一对,则实数a的取值范围是( )
| A. | [$\frac{1}{7}$,$\frac{1}{5}$]∪{3} | B. | [3,5]∪{$\frac{1}{7}$} | C. | [$\frac{1}{7}$,$\frac{1}{3}$)∪{5} | D. | [3,7)∪{$\frac{1}{5}$} |
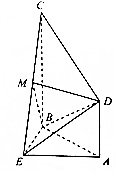 如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=$\frac{1}{2}$BC=2,M是EC的中点.
如图,在多面体ABCDE中,平面ABE⊥平面ABCD,△ABE是等边三角形,四边形ABCD是直角梯形,AB⊥AD,AB⊥BC,AB=AD=$\frac{1}{2}$BC=2,M是EC的中点.