题目内容
8.已知某次数学考试的成绩服从正态分布N(116,82),则成绩在140分以上的考生所占的百分比为( )(附:正态总体在三个特殊区间内取值的概率值①P(μ-σ<X≤μ+σ)=0.6826;②P(μ-2σ<X≤μ+2σ)=0.9544;③P(μ-3σ<X≤μ+3σ)=0.9974)
| A. | 0.3% | B. | 0.23% | C. | 1.3% | D. | 0.13% |
分析 利用变量在(μ-3σ,μ+3σ)内取值的概率约为0.9974,可得成绩在(92,140)内的考生所占百分比约为99.74%,从而可求成绩在140分以上的考生所占的百分比.
解答 解:∵数学考试的成绩服从正态分布N(116,82),
∴μ=116,σ=8
∴μ-3σ=92,μ+3σ=140
∵变量在(μ-3σ,μ+3σ)内取值的概率约为0.9974,
∴成绩在(92,140)内的考生所占百分比约为99.74%,
∴成绩在140分以上的考生所占的百分比为$\frac{1}{2}(1-99.74%)$=0.13%
故选:D.
点评 本题考查正态分布的性质,考查学生分析解决问题的能力,确定成绩在(92,140)内的考生所占百分比约为99.7%是关键.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案
相关题目
18.《九章算术》是我国古代的数字名著,书中《均属章》有如下问题:“今有五人分五钱,令上二人所得与下三人等.问各德几何.”其意思为“已知A、B、C、D、E五人分5钱,A、B两人所得与C、D、E三人所得相同,且A、B、C、D、E每人所得依次成等差数列.问五人各得多少钱?”(“钱”是古代的一种重量单位).在这个问题中,E所得为( )
| A. | $\frac{2}{3}$钱 | B. | $\frac{4}{3}$钱 | C. | $\frac{5}{6}$钱 | D. | $\frac{3}{2}$钱 |
19.过点M($\frac{\sqrt{2}}{2}$,-$\frac{\sqrt{2}}{2}$)作圆x2+y2=1的切线l,l与x轴的交点为抛物线E:y2=2px(p>0)的焦点,l与抛物线E交于A、B两点,则AB中点到抛物线E的准线的距离为( )
| A. | $\frac{5\sqrt{2}}{2}$ | B. | 3$\sqrt{2}$ | C. | $\frac{7}{2}$$\sqrt{2}$ | D. | 4$\sqrt{2}$ |
16.已知复数z=2+i,则$\frac{\overline{z}}{z}$=( )
| A. | $\frac{3}{5}$-$\frac{4}{5}$i | B. | -$\frac{3}{5}$+$\frac{4}{5}$i | C. | $\frac{5}{3}$-$\frac{4}{3}$i | D. | -$\frac{5}{3}$+$\frac{4}{3}$i |
3.集合A={x|x2-x-6≤0},B={x|x<-1},则A∩(∁RB)等于( )
| A. | {x|x>-1} | B. | {x|x≥-1} | C. | {x|-1≤x≤3} | D. | {x|-2≤x≤1} |
13.“方程f′(x)=0有解”是“函数y=f(x)有极值”的( )
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
17.已知集合A={x|y=$\sqrt{2x-{x}^{2}}$},B={y|y=2x,x∈A},则A∩B=( )
| A. | [0,1) | B. | [1,2] | C. | (2,4] | D. | [2.4] |
 在某次摸底考试中,随机抽取100个人的成绩频率分布直方图如图,若参加考试的共有4000人,那么分数在90分以上的人数约为2600人,根据频率分布直方图估计此次考试成绩的中位数为97.5.
在某次摸底考试中,随机抽取100个人的成绩频率分布直方图如图,若参加考试的共有4000人,那么分数在90分以上的人数约为2600人,根据频率分布直方图估计此次考试成绩的中位数为97.5.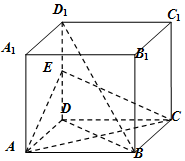 如图,在边长为2的正方体ABCD-A1B1C1D1中,E为DD1中点,
如图,在边长为2的正方体ABCD-A1B1C1D1中,E为DD1中点,