题目内容
已知数列{an}是等差数列,{bn}是等比数列,且a1=11,b1=1,a2+b2=11,a3+b3=11.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)求数列{|an-bn|}的前12项的和S12.
(Ⅰ)求数列{an}和{bn}的通项公式;
(Ⅱ)求数列{|an-bn|}的前12项的和S12.
考点:数列的求和,等差数列与等比数列的综合
专题:综合题,等差数列与等比数列
分析:(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q,依题意,得,解之即可求得数列{an}和{bn}的通项公式;
(Ⅱ)由(Ⅰ)得:|an-bn|=|13-2n-2n-1|;通过对0<n≤3与n≥4的讨论,去掉绝对值符号后分利用分组求和的方法即可求得数列{|an-bn|}的前12项的和S12.
(Ⅱ)由(Ⅰ)得:|an-bn|=|13-2n-2n-1|;通过对0<n≤3与n≥4的讨论,去掉绝对值符号后分利用分组求和的方法即可求得数列{|an-bn|}的前12项的和S12.
解答:
解:(Ⅰ)设等差数列{an}的公差为d,等比数列{bn}的公比为q,
则
,解得
,
∴an=-2n+13,bn=2n-1;
(Ⅱ)由(Ⅰ)得:|an-bn|=|13-2n-2n-1|;
(i)当0<n≤3时,an>bn,an-bn=13-2n-2n-1;
(ii)n≥4时,an<bn,|an-bn|=bn-an=2n-1-(13-2n).
∴|an-bn|=
,
∴S12=(11-1)+(9-2)+(7-4)-(5-8)-…-(-11-211)
=20+(8+16+…+211)-[5+3+…+(-11)]
=4135.
则
|
|
∴an=-2n+13,bn=2n-1;
(Ⅱ)由(Ⅰ)得:|an-bn|=|13-2n-2n-1|;
(i)当0<n≤3时,an>bn,an-bn=13-2n-2n-1;
(ii)n≥4时,an<bn,|an-bn|=bn-an=2n-1-(13-2n).
∴|an-bn|=
|
∴S12=(11-1)+(9-2)+(7-4)-(5-8)-…-(-11-211)
=20+(8+16+…+211)-[5+3+…+(-11)]
=4135.
点评:本题考查等差数列与等比数列的通项公式与求和公式,考查方程思想与分类讨论思想、等价转化思想的综合应用,属于难题.

练习册系列答案
相关题目
已知α为锐角,且sin(α-
)=
,则sinα=( )
| π |
| 4 |
| 1 |
| 3 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
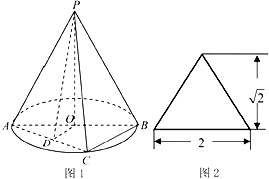 圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点
圆锥PO如图1所示,图2是它的正(主)视图.已知圆O的直径为AB,C是圆周上异于A、B的一点,D为AC的中点 如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,侧面B1C1CB⊥底面ABC,O是BC的中点,且AC1⊥BC.
如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,侧面B1C1CB⊥底面ABC,O是BC的中点,且AC1⊥BC.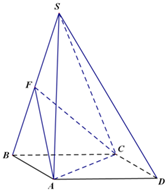 四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2
四棱锥S-ABCD,底面ABCD为平行四边形,侧面SBC⊥底面ABCD.已知∠DAB=135°,BC=2 已知函数f(x)=2cos2(
已知函数f(x)=2cos2(