题目内容
 如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,侧面B1C1CB⊥底面ABC,O是BC的中点,且AC1⊥BC.
如图,斜三棱柱ABC-A1B1C1的所有棱长均为a,侧面B1C1CB⊥底面ABC,O是BC的中点,且AC1⊥BC.(Ⅰ)求证:AC1⊥A1B;
(Ⅱ)求直线B1A与平面AOC1所成角的正切值.
考点:直线与平面所成的角
专题:空间位置关系与距离,空间角
分析:(Ⅰ)利用线面垂直证明线线垂直;
(Ⅱ)所以B1C1⊥面AOC1,所以∠B1AC1就是所求的线面角,再解三角形.
(Ⅱ)所以B1C1⊥面AOC1,所以∠B1AC1就是所求的线面角,再解三角形.
解答:
解: (Ⅰ)连接A1C,因四边形A1ACC1是菱形,所以AC1⊥A1C------------4分
(Ⅰ)连接A1C,因四边形A1ACC1是菱形,所以AC1⊥A1C------------4分
由已知AC1⊥BC且BC∩A1C=C
所以AC1⊥面A1BC------------6分
所以AC1⊥A1B;----------7分
(Ⅱ)因为AO是正△ABC的中线,所以BC⊥AO,又AC1⊥BC,所以BC⊥面AOC1-----------------9分
所以B1C1⊥面AOC1,所以∠B1AC1就是所求的线面角,----------11分
所以BC⊥C1O,
又因为侧面侧面B1C1CB⊥底面ABC,侧面B1C1CB∩底面ABC=BC
所以C1O⊥面ABC,
因为C1O=AO=
a,所以AC1=
a,-----------13分
在Rt△AB1C1中,tan∠B1AC1=
=
-----------14分
 (Ⅰ)连接A1C,因四边形A1ACC1是菱形,所以AC1⊥A1C------------4分
(Ⅰ)连接A1C,因四边形A1ACC1是菱形,所以AC1⊥A1C------------4分由已知AC1⊥BC且BC∩A1C=C
所以AC1⊥面A1BC------------6分
所以AC1⊥A1B;----------7分
(Ⅱ)因为AO是正△ABC的中线,所以BC⊥AO,又AC1⊥BC,所以BC⊥面AOC1-----------------9分
所以B1C1⊥面AOC1,所以∠B1AC1就是所求的线面角,----------11分
所以BC⊥C1O,
又因为侧面侧面B1C1CB⊥底面ABC,侧面B1C1CB∩底面ABC=BC
所以C1O⊥面ABC,
因为C1O=AO=
| ||
| 2 |
| ||
| 2 |
在Rt△AB1C1中,tan∠B1AC1=
| a | ||||
|
| ||
| 3 |
点评:本题考查直线与直线垂直的判定,线面角的计算,考查计算能力,逻辑思维能力,是中档题.

练习册系列答案
相关题目
下列说法正确的是( )
| A、函数的极大值就是函数的最大值 |
| B、函数的极小值就是函数的最小值 |
| C、函数的最值一定是极值 |
| D、在闭区间上的连续函数一定存在最值 |
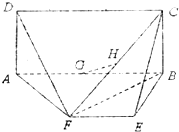 已知矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,AB∥FE,G、H分别为AB、CF的中点,AB=2,AD=EF=1,∠AFB=
已知矩形ABCD所在的平面和梯形ABEF所在的平面互相垂直,AB∥FE,G、H分别为AB、CF的中点,AB=2,AD=EF=1,∠AFB=