题目内容
1．若${（1+x）^6}{（1-2x）^5}={a_0}+{a_1}x+{a_2}{x^2}+…+{a_{11}}{x^{11}}$，求（1）a1+a2+a3+…+a11；
（2）a0+a2+a4+…+a10．
分析 用赋值法，在所给的等式中，分别令x=0和1，-1，即可求出对应的值．
解答 解：（1）令x=1，a0+a1+a2+…+a11=-64①
又令x=0，a0=1，
∴a1+a2+a3+…+a11=-65
（2）令x=-1，a0-a1+a2…-a11=0②
①+②则z（a0+a2+a4+…+a10）=-64，
∴a0+a2+a4+…+a10=-32．
点评 本题主要考查了二项式定理的应用问题，是给变量赋值的计算问题，关键是根据要求的结果，选择合适的数值代入，是基础题目．
练习册系列答案
相关题目
11．已知直线mx+4y-2=0与直线2x-5y+n=0互相垂直，垂足为（1，p），则m+n-p等于（ ）
| A． | 0 | B． | 4 | C． | 20 | D． | 24 |
12．在△ABC中，A=30°，AB=2，且△ABC的面积为$\sqrt{3}$，则△ABC外接圆的半径为（ ）
| A． | $\frac{2\sqrt{3}}{3}$ | B． | $\frac{4\sqrt{3}}{3}$ | C． | 2 | D． | 4 |
9．在等差数列{an}中，a5=9，且2a3=a2+6，则a1等于（ ）
| A． | -3 | B． | -2 | C． | 0 | D． | 1 |
19．
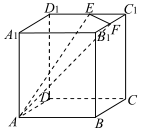如图所示，在棱长为 6的正方体ABCD-A1B1C1D1中，点E，F分别是棱C1D1，B1C1的中点，过A，E，F三点作该正方体的截面，则截面的周长为（ ）
如图所示，在棱长为 6的正方体ABCD-A1B1C1D1中，点E，F分别是棱C1D1，B1C1的中点，过A，E，F三点作该正方体的截面，则截面的周长为（ ）| A． | $18+3\sqrt{2}$ | B． | $6\sqrt{13}+3\sqrt{2}$ | C． | $6\sqrt{5}+9\sqrt{2}$ | D． | $10+3\sqrt{2}+4\sqrt{10}$ |