题目内容
11.已知直线mx+4y-2=0与直线2x-5y+n=0互相垂直,垂足为(1,p),则m+n-p等于( )| A. | 0 | B. | 4 | C. | 20 | D. | 24 |
分析 先由两直线平行斜率相等,求出m,第一直线的方程确定了,把垂足坐标代入,可求p,垂足坐标确定了,把垂足坐标代入第二条直线的方程可得 n,进而求得m+n-p的值.
解答 解:∵直线mx+4y-2=0与2x-5y+n=0互相垂直,
∴$\frac{m}{-4}$×$\frac{2}{5}$=-1,
∴m=10,
直线mx+4y-2=0 即 5x+2y-1=0,
垂足(1,p)代入得,5+2p-1=0,
∴p=-2.
把P(1,-2)代入2x-5y+n=0,
可得 n=-12,
∴m+n-p=10-12+2=0,
故选:A.
点评 本题考查两直线垂直的性质,垂足是两直线的公共点,垂足坐标同时满足两直线的方程.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
1.已知i是虚数单位,复数z满足z=i(i-1),则z的虚部是( )
| A. | 1 | B. | -1 | C. | i | D. | -i |
2.如图,△A'B'C'是△ABC的直观图,其中A'B'=A'C',那么△ABC是( )
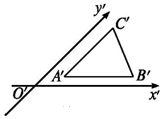

| A. | 等腰三角形 | B. | 直角三角形 | C. | 等腰直角三角形 | D. | 钝角三角形 |
3.已知集合A={1,2,3,4,5,6},B={3,4,5,6,7,8},在集合A∪B中任取一个元素,则该元素是集合A∩B中的元素的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{3}{7}$ | C. | $\frac{5}{8}$ | D. | $\frac{1}{2}$ |
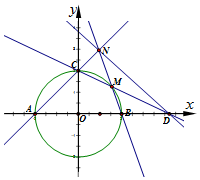 如图,圆O:x2+y2=4与坐标轴交于点A,B,C.设点M是圆上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.
如图,圆O:x2+y2=4与坐标轴交于点A,B,C.设点M是圆上任意一点(不在坐标轴上),直线CM交x轴于点D,直线BM交直线AC于点N.