题目内容
已知△ABC的三边分别是a，b，c，且满足b2+c2=bc+a2
（1）求角A；
（2）若a=2，求△ABC的面积的最大值．
（1）求角A；
（2）若a=2，求△ABC的面积的最大值．
考点：余弦定理
专题：解三角形
分析：（1）根据余弦定理直接求解即可求角A；
（2）若a=2，根据三角形的面积公式结合基本不等式的性质即可求△ABC的面积的最大值．
（2）若a=2，根据三角形的面积公式结合基本不等式的性质即可求△ABC的面积的最大值．
解答：
解：（1）由余弦定理得cosA=
=
，则A=
；
（2）由题得b2+c2=bc+4≥2bc⇒bc≤4，
则S△ABC=
bcsinA≤
(b=c时取等号）
故△ABC的面积的最大值为
．
| b2+c2-a2 |
| 2bc |
| 1 |
| 2 |
| π |
| 3 |
（2）由题得b2+c2=bc+4≥2bc⇒bc≤4，
则S△ABC=
| 1 |
| 2 |
| 3 |
故△ABC的面积的最大值为
| 3 |
点评：本题主要考查余弦定理的应用，比较基础．
练习册系列答案
名校课堂系列答案
相关题目
如图是一个算法流程图，则输出的x的值是
如图，已知⊙O的半径为2，PA是⊙O的切线，A为切点，且PA=2一只蜜蜂在一个棱长为5的正方体内自由飞行，若蜜蜂在飞行过程中始终保持与正方体6个表面的距离均大于2，称其为“安全飞行”，则蜜蜂“安全飞行”的概率为（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
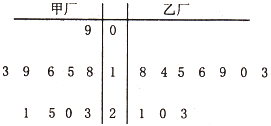为了解甲、乙两厂的产品质量，分别从两厂生产的产品中各随机抽取10件，测量产品中某种元素的含量（单位：毫克），其测量数据的茎叶图如图所示：规定：当产品中此种元素含量大于18毫克时，认定该产品为优等品．