题目内容
已知函数y=
在（-∞，-1）上单调递减，则实数a的取值范围是 ．
| 2x+a |
| x+1 |
考点：函数单调性的判断与证明
专题：函数的性质及应用
分析：当x＜-1时，函数的导数f′（x）＜0，解不等式求得a的范围．
解答：
解：由题意可得，当x＜-1时，函数的导数f′（x）=
＜0，解得a＞2．
故a的范围是（2，+∞），
故答案为：（2，+∞）．
| 2(x+1)-(2x+a) |
| (x+1)2 |
故a的范围是（2，+∞），
故答案为：（2，+∞）．
点评：本题主要考查函数的单调性与导数的关系，求函数的导数，属于中档题．
练习册系列答案
字词句段篇系列答案
相关题目
已知函数f（x）=2sin（
x+
），则f（1）+f（2）+…+f（2012）+f（2013）的值是（ ）
| π |
| 3 |
| 2π |
| 3 |
A、-2
| ||
B、-
| ||
C、
| ||
| D、0 |
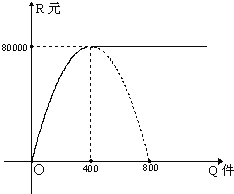某工厂生产某种产品，固定成本为20000元，每生产一件产品，成本增加100元．已知总收益R是年产量Q（件）的函数，其图象（图中实线部分）如下：当年产量Q在[0，400]内时，为抛物线的一段；当年产量Q＞400件时，为一条射线．