题目内容
13.已知正项数列{an}的前n项和为Sn,记bn=$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$(n∈N*),数列{bn}的前n项和为Tn,若对任意正整数n恒有2Sn=a${\;}_{n}^{2}$+an成立,则T48=6.分析 对任意正整数n恒有2Sn=a${\;}_{n}^{2}$+an成立,可得a1=1.当n≥2时,an-an-1=1,利用等差数列的通项公式可得an=n,可得bn=$\frac{1}{\sqrt{n}+\sqrt{n+1}}$=$\sqrt{n+1}$-$\sqrt{n}$,再利用“累加求和”即可得出.
解答 解:对任意正整数n恒有2Sn=a${\;}_{n}^{2}$+an成立,
∴2a1=${a}_{1}^{2}$+a1,a1>0,解得a1=1.
当n≥2时,2an=2(Sn-Sn-1)=${a}_{n}^{2}+{a}_{n}$-$({a}_{n-1}^{2}+{a}_{n-1})$,
化为:(an+an-1)(an-an-1-1)=0,an>0,
∴an-an-1=1,
∴数列{an}是等差数列,首项为1,公差为1.
∴an=1+(n-1)=n.
∴bn=$\frac{1}{\sqrt{{a}_{n}}+\sqrt{{a}_{n+1}}}$=$\frac{1}{\sqrt{n}+\sqrt{n+1}}$=$\sqrt{n+1}$-$\sqrt{n}$,
∴数列{bn}的前n项和为Tn=$(\sqrt{2}-1)$+$(\sqrt{3}-\sqrt{2})$+…+$(\sqrt{n+1}-\sqrt{n})$=$\sqrt{n+1}$-1.
∴T48=$\sqrt{49}$-1=6.
故答案为:6.
点评 本题考查了递推关系、等差数列的通项公式、“累加求和”方法,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
1.如图是一个程序框图,若输出i的值为5,则实数m的值可以是( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
8.已知函数f(x)是定义在R上的奇函数,当x≤0时,f(x)=x(1-x),若数列{an}满足a1=$\frac{1}{2}$,且an+1=$\frac{1}{1-{a}_{n}}$,则f(-a2016)( )
| A. | 2 | B. | -2 | C. | 6 | D. | -6 |
5. 执行如图所示的程序框图,若输入a=7,b=1,则输出S的值为( )
执行如图所示的程序框图,若输入a=7,b=1,则输出S的值为( )
 执行如图所示的程序框图,若输入a=7,b=1,则输出S的值为( )
执行如图所示的程序框图,若输入a=7,b=1,则输出S的值为( )| A. | 16 | B. | 19 | C. | 34 | D. | 50 |

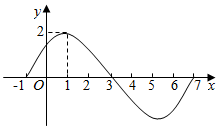 下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).
下图为函数y=Asin(ωx+φ)的一段图象,已知A>0,ω>0,φ∈(-$\frac{π}{2}$,$\frac{π}{2}$).