题目内容
17.已知函数f(x)=lnx-a(x-1),a∈R.(Ⅰ)求函数f(x)在点(1,f(1))点处的切线方程;
(Ⅱ)当x≥1时,f(x)≤$\frac{lnx}{x+1}$恒成立,求a的取值范围.
分析 (I)先求出切线的斜率k=f′(1)和f(1),代入直线的点斜式方程化简即可;
(II)作差得f(x)-$\frac{lnx}{x+1}$=$\frac{xlnx-a({x}^{2}-1)}{x+1}$,令g(x)=xlnx-a(x2-1)(x≥1),依次计算g′(x),g″(x),讨论a的范围判断g(x)的单调性,验证结论是否成立即可得出a的范围.
解答 解:(I)∵f(x)=lnx-a(x-1),∴f′(x)=$\frac{1}{x}$-a,
∴f(1)=0,f′(1)=1-a,
∴函数f(x)在点(1,f(1))点处的切线方程为y=(1-a)(x-1).
(II)f(x)-$\frac{lnx}{x+1}$=$\frac{xlnx-a({x}^{2}-1)}{x+1}$,令g(x)=xlnx-a(x2-1)(x≥1),
则g′(x)=lnx+1-2ax,g″(x)=$\frac{1}{x}-2a$=$\frac{1-2ax}{x}$,
①若a≤0,则g″(x)>0,∴g′(x)在[1,+∞)上单调递增,
∴g′(x)≥g′(1)=1-2a>0,
∴g(x)在[1,+∞)上单调递增,
∴g(x)≥g(1)=0,∴$\frac{xlnx-a({x}^{2}-1)}{x+1}$≥0,
即f(x)-$\frac{lnx}{x+1}$≥0,不符合题意.
②若0$<a<\frac{1}{2}$,则当x∈(1,$\frac{1}{2a}$)时,g″(x)>0,
∴g′(x)在[1,$\frac{1}{2a}$)上单调递增,
∴g′(x)≥g′(1)=1-2a>0,
∴g(x)在[1,+∞)上单调递增,
∴g(x)≥g(1)=0,∴$\frac{xlnx-a({x}^{2}-1)}{x+1}$≥0,
即f(x)-$\frac{lnx}{x+1}$≥0,不符合题意.
③若a$≥\frac{1}{2}$,则当x∈[1,+∞)上时,g″(x)≤0,
∴g′(x)在[1,+∞)上单调递减,
∴g′(x)≤g′(1)=1-2a≤0,
∴g(x)在[1,+∞)上单调递减,
∴g(x)≤g(1)=0,∴$\frac{xlnx-a({x}^{2}-1)}{x+1}$≤0,
即f(x)≤$\frac{lnx}{x+1}$,符合题意.
综上所述,a的取值范围是[$\frac{1}{2}$,+∞).
点评 本题考查了导数的几何意义,导数与函数的单调性的关系,分类讨论思想,属于中档题.

| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | -$\frac{4}{3}$ | D. | -$\frac{3}{4}$ |
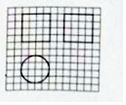 如图,网络纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三观图,切削该毛坯得到一个表面积最大的长方体,则该长方体的表面积为( )
如图,网络纸上正方形小格的边长为1,图中粗线画出的是某几何体毛坯的三观图,切削该毛坯得到一个表面积最大的长方体,则该长方体的表面积为( )| A. | 24 | B. | 16+32$\sqrt{2}$ | C. | 16+8$\sqrt{2}$ | D. | 32 |
| A. | 1050辆 | B. | 1350辆 | C. | 1650辆 | D. | 1950辆 |
| A. | y=sin($\frac{x}{2}$+$\frac{π}{6}$) | B. | y=cos(2x+$\frac{π}{3}$) | C. | y=sin(2x-$\frac{π}{6}$) | D. | y=cos($\frac{x}{2}$-$\frac{π}{6}$) |