题目内容
2．
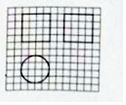如图，网络纸上正方形小格的边长为1，图中粗线画出的是某几何体毛坯的三观图，切削该毛坯得到一个表面积最大的长方体，则该长方体的表面积为（ ）| A． | 24 | B． | 16+32$\sqrt{2}$ | C． | 16+8$\sqrt{2}$ | D． | 32 |
分析 由三视图可得，直观图是底面直径、高都为4的圆柱，切削该毛坯得到一个表面积最大的长方体，长方体的底面为边长为2$\sqrt{2}$的正方体，即可求出长方体的表面积．
解答 解：由三视图可得，直观图是底面直径、高都为4的圆柱，切削该毛坯得到一个表面积最大的长方体，长方体的底面为边长为2$\sqrt{2}$的正方体，该长方体的表面积为$2×（2\sqrt{2}）^{2}+4×2\sqrt{2}×4$=16+32$\sqrt{2}$，
故选B．
点评 本题考查三视图，考查表面积的计算，考查学生分析解决问题的能力，属于中档题．
练习册系列答案
新题型全程检测期末冲刺100分系列答案
相关题目
13．2016年美国总统大选过后，有媒体从某公司的全体员工中随机抽取了200人，对他们的投票结果进行了统计（不考虑弃权等其他情况），发现支持希拉里的一共有95人，其中女员工55人，支持特朗普的男员工有60人．
（Ⅰ）根据已知条件完成下面的2×2列联表：
（Ⅱ）根据表格中的数据，是否有95%的把握认为投票结果与性别有关？
附：
（参考公式：K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d）
（Ⅰ）根据已知条件完成下面的2×2列联表：
| 支持希拉里 | 支持特朗普 | 合计 | |
| 男员工 | |||
| 女员工 | |||
| 合计 |
附：
| P（K2≥k0） | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| K0 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
12．
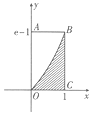图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成，现向矩形区域OABC内随机投掷一点，则该点落在非阴影区域的概率是（ ）
图所示的阴影部分由坐标轴、直线x=1及曲线y=ex-lne围成，现向矩形区域OABC内随机投掷一点，则该点落在非阴影区域的概率是（ ）| A． | $\frac{1}{e}$ | B． | $\frac{1}{e-1}$ | C． | 1-$\frac{1}{e}$ | D． | 1-$\frac{1}{e-1}$ |