题目内容
15.集合M={x|log2(1-x)<0},集合N={x|-1≤x≤1},则M∩N等于( )| A. | [-1,1) | B. | [0,1) | C. | [-1,1] | D. | (0,1) |
分析 化简集合M、N,根据交集的定义写出M∩N即可.
解答 解:集合M={x|log2(1-x)<0}
={x|1>1-x>0}
={x|0<x<1}
=(0,1);
集合N={x|-1≤x≤1}
=[-1,1];
所以M∩N=(0,1).
故选:D.
点评 本题考查了集合的化简与运算问题,是基础题目.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知定义在R上的函数f(x)满足f(x+y)=f(x)+f(y)+4xy,f(1)=1,则f(-2)=( )
| A. | -2 | B. | 2 | C. | 6 | D. | 10 |
10.已知函数f(x)=$\left\{\begin{array}{l}ln({1-x}),x<0\\{({x-1})^3}+1,x≥0\end{array}$,若f(x)≥ax恒成立,则实数a的取值范围是( )
| A. | $[{0,\frac{2}{3}}]$ | B. | $[{0,\frac{3}{4}}]$ | C. | [0,1] | D. | $[{0,\frac{3}{2}}]$ |
5.直线x+ay+6=0与直线(a-2)x+3y+2a=0平行,则a的值为( )
| A. | 3 或-1 | B. | 3 | C. | -1 | D. | $\frac{1}{2}$ |
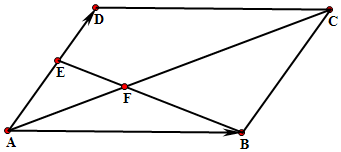 如图,平行四边形ABCD中,点E在线段AD上,BE与AC交于点F,设$\overrightarrow{AB}=a,\overrightarrow{AD}=b$.
如图,平行四边形ABCD中,点E在线段AD上,BE与AC交于点F,设$\overrightarrow{AB}=a,\overrightarrow{AD}=b$.