题目内容
2.函数f(x)=ex-2x+a,若关于x的方程f(x)=0有两个不同正根,则实数a的取值范围是(-1,2ln2-2).分析 求导f′(x)=ex-2,从而可得f(x)的单调性,从而由单调性确定函数的极值即可.
解答 解:∵f(x)=ex-2x+a,
∴f′(x)=ex-2,
∴当x∈(-∞,ln2)时,f′(x)<0,
故f(x)在(-∞,ln2)上单调递减,
当x∈(ln2,+∞)时,f′(x)>0,
故f(x)在(ln2,+∞)上单调递增,
而f(0)=1+a,f(ln2)=2-2ln2+a,$\underset{lim}{x→+∞}$f(x)=+∞;
故2-2ln2+a<0<1+a,
故a∈(-1,2ln2-2).
故答案为:(-1,2ln2-2).
点评 本题考查了导数的综合应用及分类讨论的思想应用,同时考查了方程的根与函数的零点的关系应用.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
12.函数f(x)=x3+x-3的一个零点所在的区间为( )
| A. | (0,$\frac{1}{2}$) | B. | ($\frac{1}{2}$,1) | C. | (1,$\frac{3}{2}$) | D. | ($\frac{3}{2}$,2) |
10.用“辗转相除法”求得333和481的最大公约数是( )
| A. | 3 | B. | 9 | C. | 37 | D. | 51 |
17.已知顶点在原点,关于y轴对称的抛物线与直线x-2y=1交于P,Q两点,若|PQ|=$\sqrt{15}$,则抛物线的方程为( )
| A. | x2=-4y | B. | x2=12y | C. | x2=-4y或x2=12y | D. | 以上都不是 |
7.已知角α的终边经过点(3a,-4a)(a<0),则sinα+cosα等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{7}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{7}{5}$ |
12.当K2>6.635时,认为事件A与事件B( )
| A. | 有95%的把握有关 | B. | 有99%的把握有关 | ||
| C. | 没有理由说它们有关 | D. | 不确定 |
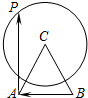 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].