题目内容
3.已知$f(x)=2sin({x+\frac{π}{3}})({x∈R})$,函数y=f(x+φ)(|φ|≤$\frac{π}{2}$)的图象关于直线x=0对称,则φ的值为$\frac{π}{6}$.分析 由条件利用正弦函数的图象的对称性,可得sin(φ+$\frac{π}{3}$)=±1,故φ+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,由此求得φ的值.
解答 解:∵函数y=f(x+φ)=2sin(x+φ+$\frac{π}{3}$)(|φ|≤$\frac{π}{2}$)的图象关于直线x=0对称,
∴sin(φ+$\frac{π}{3}$)=±1,∴φ+$\frac{π}{3}$=kπ+$\frac{π}{2}$,k∈Z,
则φ=$\frac{π}{6}$,
故答案:$\frac{π}{6}$.
点评 本题主要考查正弦函数的图象的对称性,属于基础题.

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
8.已知集合U={a,b,c,d,e },A={a,b,c },B={ b,c,d },则A∩∁UB( )
| A. | {a} | B. | {a,b,c,d } | C. | {b,c,d } | D. | {a,e } |
15.直线a∥平面α,直线b⊥平面α,则下列说法正确的是( )
| A. | a∥b | B. | a⊥b | C. | a⊥b且异面 | D. | a⊥b且相交 |
12.当K2>6.635时,认为事件A与事件B( )
| A. | 有95%的把握有关 | B. | 有99%的把握有关 | ||
| C. | 没有理由说它们有关 | D. | 不确定 |
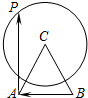 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].