题目内容
19.已知直线y=kx+m(m≠0)与圆x2+y2=169有公共点,且公共点的横坐标和纵坐标均为整数,那么这样的直线共有( )| A. | 60条 | B. | 66条 | C. | 72条 | D. | 78条 |
分析 直线是截距式方程,因而不平行坐标轴,不过原点,考查圆上横坐标和纵坐标均为整数的点的个数,结合排列组合知识分类解答.
解答 解:可知直线的横、纵截距都不为零,即与坐标轴不垂直,不过坐标原点,而圆x2+y2=169上的整数点共有12个,分别为(5,±12),(-5,±12),(12,±5),(-12,±5),(±13,0),(0,±13),
前8个点中,过任意一点的圆的切线满足,有8条;
12个点中过任意两点,构成C122=66条直线,其中有4条直线垂直x轴,有4条直线垂直y轴,还有6条过原点(圆上点的对称性),
故满足题设的直线有52条.
综上可知满足题设的直线共有52+8=60条,
故选:A.
点评 此题考查了直线与圆相交的性质,是以直线和圆为载体,考查数学的综合应用能力.学生做题时一定要注意与y轴平行的直线斜率不存在不满足题意,要舍去.

练习册系列答案
 导学教程高中新课标系列答案
导学教程高中新课标系列答案 小学课时特训系列答案
小学课时特训系列答案
相关题目
10.用“辗转相除法”求得333和481的最大公约数是( )
| A. | 3 | B. | 9 | C. | 37 | D. | 51 |
7.已知角α的终边经过点(3a,-4a)(a<0),则sinα+cosα等于( )
| A. | $\frac{1}{5}$ | B. | $\frac{7}{5}$ | C. | -$\frac{1}{5}$ | D. | -$\frac{7}{5}$ |
8.已知集合U={a,b,c,d,e },A={a,b,c },B={ b,c,d },则A∩∁UB( )
| A. | {a} | B. | {a,b,c,d } | C. | {b,c,d } | D. | {a,e } |
9.把二进制数10102化为十进制数为( )
| A. | 20 | B. | 12 | C. | 11 | D. | 10 |
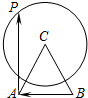 如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].
如图所示,△ABC是边长为4的等边三角形,点P是以点C为圆心、3为半径的圆上的任意一点,则$\overrightarrow{BA}•\overrightarrow{AP}$的取值范围是[-20,4].