题目内容
13.四棱锥S-ABCD的底面是边长为4$\sqrt{2}$的正方形,且SA=SB=SC=SD=4$\sqrt{5}$,则过点A,B,C,D,S的球的体积为$\frac{500}{3}$π.分析 作出直观图,根据所给条件寻找外接球的球心位置,计算球的半径.
解答  解:取底面中心O,则OA=OB=OC=OD=4,SO⊥平面ABCD,
解:取底面中心O,则OA=OB=OC=OD=4,SO⊥平面ABCD,
∴SO=8,
设过点A,0B,C,D,S的球的半径为R,则
R2=(8-R)2+42,
∴R=5
∴过点A,B,C,D,S的球的体积为V=$\frac{4}{3}$π×53=$\frac{500}{3}$π.
故答案为:$\frac{500}{3}$π.
点评 本题考查了球与内接多面体的关系,求出外接球的半径是解题关键.

练习册系列答案
相关题目
3.下列不等式中,①α∈(0,$\frac{π}{2}$)时,sin2α+$\frac{4}{{{{sin}^2}α}}$≥4;②log2(x2+1)≥1+log2x(x>0);③sinx+cosx≤$\sqrt{2}$;④22x+22y≥2x+y+1恒成立的有( )
| A. | ①②③ | B. | ①②④ | C. | ①③④ | D. | ②③④ |
8.北京市人社局今日发布了“关于公布2015年度北京市职工平均工资的通知”,透露2015年度全市职工平均工资为85038元,月平均工资7086元,某网站整理了2011-2015年北京市职工年平均工资,如表,网友纷纷吐槽:“对不起,我又拖后腿了”“还没赶上去年的平均值,你们又涨了…”“我周围很多人这5年工资都没变过,这数据肯定有问题”
(1)根据上表所给信息估计:到2020年,北京市职工税前平均年薪能否比2011年翻翻?,并简要说明.
(2)使用你所学的概率统计知识,解释大多数人认为自己工资为达到平均值的理由:
(3)你能否向人社局提出一些建议来改进统计方案,是大部分人认为公布的结果与自己的实际工资水平相差不大.
| 2011-2015年北京市职工年平均工资(税前:单位:元) | |
| 时间 | 平均年薪 |
| 2011 | 56061 |
| 2012 | 62677 |
| 2013 | 69521 |
| 2014 | 77560 |
| 2015 | 85038 |
(2)使用你所学的概率统计知识,解释大多数人认为自己工资为达到平均值的理由:
(3)你能否向人社局提出一些建议来改进统计方案,是大部分人认为公布的结果与自己的实际工资水平相差不大.
5.根据统计数据,某产品的销售额y对广告费用x(单位:百万元)的线性回归方程为y=5.7x+18.6,则下列说法不正确的是( )
| A. | 若下一销售季再投入5百万元广告费,则估计销售额约可达47.1百万元 | |
| B. | 已知统计数据中的平均销售额为41.4百万元,则平均广告费为4百万元 | |
| C. | 广告费用x和销售额y之间的相关系数不能确定正负,但其绝对值趋于1 | |
| D. | 5.7的含义是广告费用每增加1百万元,销售额大约增长5.7百万元左右 |
2.已知函数f(x)=a-x+xex,若存在x0>-1,使得f(x0)≤0,则实数a的取值范围为( )
| A. | [0,+∞) | B. | (-∞,0] | C. | [1,+∞) | D. | (-∞,1] |
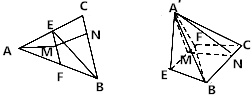 如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.
如图,已知等边△ABC中,E,F分别为AB,AC边的中点,N为BC边上一点,且CN=$\frac{1}{4}$BC,将△AEF沿EF折到△A′EF的位置,使平面A′EF⊥平面EF-CB,M为EF中点.