题目内容
 如图,平面α与平面β交于直线l,A,C是平面α内不同的两点,B,D是平面β内不同的两点,且A,B,C,D不在直线l上,M,N分别是线段AB,CD的中点,下列判断错误的是
如图,平面α与平面β交于直线l,A,C是平面α内不同的两点,B,D是平面β内不同的两点,且A,B,C,D不在直线l上,M,N分别是线段AB,CD的中点,下列判断错误的是①若AB与CD相交,且直线AC平行于l时,则直线BD与l可能平行也有可能相交
②若AB,CD是异面直线时,则直线MN可能与l平行
③若存在异于AB,CD 的直线同时与直线AC,MN,BD都相交,则AB,CD不可能是异面直线
④M,N两点可能重合,但此时直线AC与l不可能相交.
考点:与二面角有关的立体几何综合题
专题:综合题,空间位置关系与距离
分析:①当AB与CD相交,直线AC平行于l时,直线BD可以与l平行;②AB,CD是异面直线时,MN不可能与l平行;③若存在异于AB,CD 的直线同时与直线AC,MN,BD都相交,则AB,CD可能是异面直线;④若M,N两点可能重合,则AC∥BD,故AC∥l,此时直线AC与直线l不可能相交.
解答:
解:对于①,因为AB与CD相交,则ABCD四点共面于平面γ,且λ∩β=BD,λ∩α=AC,由AC∥l,可得AC∥β,
由线面平行的性质可得AC∥BD,进而可得BD∥l,故①错误;
对于②,当AB,CD是异面直线时,MN不可能与l平行,过N作CD的平行线EF,分别交α,β于E、F,可得M为EF中点,可得△BMF≌△AME,可得AE∥BF,显然与题设矛盾,故②错误;
对于③,若存在异于AB,CD 的直线同时与直线AC,MN,BD都相交,则AB,CD可能是异面直线,故③错误;
对于④,若M,N两点可能重合,则AC∥BD,故AC∥l,故此时直线AC与直线l不可能相交,故④正确.
故答案为:①②③.
由线面平行的性质可得AC∥BD,进而可得BD∥l,故①错误;
对于②,当AB,CD是异面直线时,MN不可能与l平行,过N作CD的平行线EF,分别交α,β于E、F,可得M为EF中点,可得△BMF≌△AME,可得AE∥BF,显然与题设矛盾,故②错误;
对于③,若存在异于AB,CD 的直线同时与直线AC,MN,BD都相交,则AB,CD可能是异面直线,故③错误;
对于④,若M,N两点可能重合,则AC∥BD,故AC∥l,故此时直线AC与直线l不可能相交,故④正确.
故答案为:①②③.
点评:本题主要考查空间直线位置关系的判断,考查图形的观察能力与运用相关知识证明判断的能力.综合性较强.

练习册系列答案
相关题目
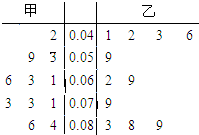 PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,如图,则甲、乙两地所测数据的中位数较低的是( )
PM2.5是指大气中直径小于或等于2.5微米的颗粒物,也称为可入肺颗粒物.根据北京某日早7点至晚8点甲、乙两个PM2.5监测点统计的数据(单位:毫克/每立方米)列出的茎叶图,如图,则甲、乙两地所测数据的中位数较低的是( )| A、甲 | B、乙 |
| C、甲乙相等 | D、无法确定 |
| cos2600° |
A、
| ||||
B、-
| ||||
C、
| ||||
D、-
|
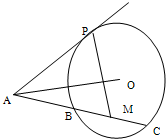 (几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为
(几何证明选讲)已知AP是圆O的切线,AC是圆O的割线,与圆交于B,C两点,点M是弦BC的中点,若圆心O在∠PAB的内部,如图,则∠OAM+∠APM的大小为