题目内容
2.方程lgx=-x2+18x-80的解的个数为2.分析 根据函数与方程的关系作出函数y=lgx和y=-x2+18x-80的图象,利用数形结合进行判断即可.
解答  解:设y=lgx和y=-x2+18x-80,
解:设y=lgx和y=-x2+18x-80,
作出两个函数的图象如图:
则函数y=-x2+18x-80的对称轴为x=9,此时函数取得最大值y=1,
而y=lg9<1,
在两个函数有2个交点,
即方程lgx=-x2+18x-80的解的个数为2个,
故答案为:2.
点评 本题主要考查函数与方程的关系,根据条件转化为两个函数的交点个数问题是解决本题的关键.

练习册系列答案
相关题目
17.若cos($\frac{π}{6}$-α)=$\frac{1}{3}$,则cos($\frac{5π}{6}$+α)-cos($\frac{4π}{3}$-2α)=( )
| A. | -$\frac{10}{9}$ | B. | $\frac{10}{9}$ | C. | $\frac{4}{5}$ | D. | -$\frac{4}{5}$ |
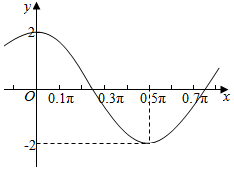 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.