题目内容
13.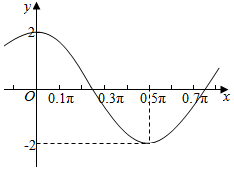 已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象如图所示.(1)求A,ω,φ的值;
(2)若y=1,求对应x的值.
分析 (1)由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,可得函数的解析式.
(2)由题意可得cos2x=$\frac{1}{2}$,此时,2x=2kπ±$\frac{π}{3}$,从而求得x的值.
解答 解:(1)结合函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<π)的图象,
可得A=2,$\frac{1}{2}$•$\frac{2π}{ω}$=0.5π,∴ω=2.
再结合五点法作图可得0+φ=$\frac{π}{2}$,∴φ=$\frac{π}{2}$,即y=2sin(2x+$\frac{π}{2}$)=2cos2x.
(2)令y=1,可得cos2x=$\frac{1}{2}$.此时,2x=2kπ±$\frac{π}{3}$,即x=kπ±$\frac{π}{6}$,k∈Z.
点评 本题主要考查由函数y=Asin(ωx+φ)的部分图象求解析式,由函数的最值求出A,由周期求出ω,由五点法作图求出φ的值,根据三角函数的值求角,属于基础题.

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
4.执行如图所示的程序框图,如果输入的x∈[0,3],则输出的结果为( )


| A. | (5,10] | B. | [3,5) | C. | [3,10] | D. | [5,10] |
1.已知直角梯形ABCD中,AB⊥AD,AB=2,DC=1,AB∥DC,则当AC⊥BC时,AD=( )
| A. | 1 | B. | $\sqrt{2}$ | C. | $\sqrt{3}$ | D. | 2 |