题目内容
9.某商店销售茶壶和茶杯,茶壶每个定价为20元,茶杯每个定价为5元.现该店推出两种优惠办法:(1)买一个茶壶赠送一个茶杯;
(2)按购买总价的92%付款.
某顾客需购买茶壶4个,茶杯若干个(不少于4个),试建立在两种优惠办法下,付款y(元)与购买茶杯个数x(个)之间的函数关系式,由此能否决定选择哪种优惠办法省钱?
分析 根据购买的总费用=茶壶的费用+茶杯的费用,建立关系式就可以了;分3种情况讨论,当y1>y2,y1=y2,y1<y2时分别求出x的值即可.
解答 解:优惠办法(1):y1=4×20+(x-4)×5=5x+60(x≥4,x∈N*),
优惠办法(2):y2=0.92(4×20+5x)=4.6x+73.6(x≥4,x∈N*)
当y1=y2,5x+60=4.6x+73.6,解得:x=34
∵x≥4,x∈N*,
∴当4≤x<34时,优惠办法(1)省钱;当x=34时,两种方法一样优惠;当x>34时,优惠办法(2)省钱.
点评 本题考查了单价×数量=总价的运用,一次函数的解析式的运用,方案设计的运用,解答时求出函数的解析式是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
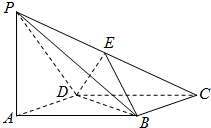 如图,四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为菱形,E为侧棱PC上一点.
如图,四棱锥P-ABCD中,侧棱PA⊥底面ABCD,底面ABCD为菱形,E为侧棱PC上一点. 如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y.
如图,有一块半径为2的半圆形纸片,计划剪裁成等腰梯形ABCD的形状,它的下底AB是⊙O的直径,上底CD的端点在圆周上,设CD=2x,梯形ABCD的周长为y. 如图,在正方体ABCD-A1B1C1D1中,点E,F分别是上底面A1B1C1D1和侧面CDD1C1的中心.
如图,在正方体ABCD-A1B1C1D1中,点E,F分别是上底面A1B1C1D1和侧面CDD1C1的中心.