题目内容
18.椭圆E的左右焦点为F1,F2,E上一点P到F1距离的最大值为7,最小值为1,则椭圆E的离心率的算术平方根为( )| A. | $\frac{1}{2}$ | B. | $\frac{{\sqrt{2}}}{2}$ | C. | $\frac{{\sqrt{3}}}{2}$ | D. | $\frac{1}{7}$ |
分析 利用椭圆的性质求出a,c,然后求解离心率,推出结果即可.
解答 解:椭圆E:的左右焦点为F1,F2,E上一点P到F1距离的最大值为7,最小值为1,
可得a+c=7,a-c=1,则a=4,c=3,
椭圆的离心率为:$\frac{c}{a}$=$\frac{3}{4}$,
则椭圆E的离心率的算术平方根为:$\frac{\sqrt{3}}{2}$.
故选:C.
点评 本题考查椭圆的简单性质的应用,考查计算能力.

练习册系列答案
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案
相关题目
5.已知x<0,则$y=3x+\frac{4}{x}$有( )
| A. | 最大值$-4\sqrt{3}$ | B. | 最小值$-4\sqrt{3}$ | C. | 最大值$4\sqrt{3}$ | D. | 最小值$4\sqrt{3}$ |
 的图像与
的图像与 的图像关于直线
的图像关于直线 对称,且
对称,且 ,则
,则 ( )
( ) B.
B. C.
C. D.
D.
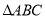 中,
中,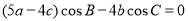 .
.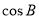 的值;
的值;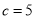 ,b=
,b=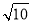 ,求
,求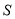 .
.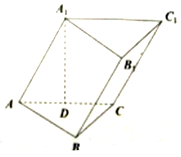 如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.
如图,在斜三棱柱ABC-A1B1C1中,侧面ACC1A1是边长为4的菱形,BC⊥平面ACC1A1,CB=2,点A1在底面ABC上的射影D为棱AC的中点,点A在平面A1CB内的射影为E.