题目内容
5．在直角坐标平面xoy上，由不等式组$\left\{\begin{array}{l}{|x|≤2}\\{|y|≤2}\\{||x|-|y||≤1}\end{array}\right.$确定的区域面积为12．分析 作出不等式组所表示的平面区域，利用正方形的面积减去4个三角形的面积即可．
解答 
解：作出不等式组$\left\{\begin{array}{l}{|x|≤2}\\{|y|≤2}\\{||x|-|y||≤1}\end{array}\right.$所表示的平面区域如同所示的正方形，去掉四个等腰直角三角形，
由题意：S=4×4-4S△=16-4×$\frac{1}{2}×2×1$=12．
故答案为：12．
点评 本题主要考查了一般图形的面积求解的转化，解题的关键是根据题意作出不等式组所表示的平面区域，把不规则图形的面积转化为三角形的面积．
练习册系列答案
相关题目
13．方程x2+y2+Dx+Ey+F=0表示以（-2，3）为圆心，4为半径的圆，则D，E，F的值分别为（ ）
| A． | 4，-6，3 | B． | -4，6，3 | C． | -4，-6，3 | D． | 4，-6，-3 |
20．点（-1，-1）在圆（x+a）2+（y-a）2=4的内部，则a的取值范围是（ ）
| A． | -1＜a＜1 | B． | 0＜a＜1 | C． | a＜-1或a＞1 | D． | a=±1 |
10．
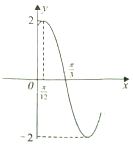函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，把f（x）的图象向右平移$\frac{π}{3}$个单位长度得到g（x）的图象，则g（x）的单调递增区间是（ ）
函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，|φ|＜$\frac{π}{2}$）的部分图象如图所示，把f（x）的图象向右平移$\frac{π}{3}$个单位长度得到g（x）的图象，则g（x）的单调递增区间是（ ）| A． | $[{kπ-\frac{5π}{12}，kπ+\frac{π}{12}}]，k∈z$ | B． | $[{kπ-\frac{π}{6}，kπ+\frac{π}{3}}]，k∈z$ | ||
| C． | $[{kπ-\frac{π}{12}，kπ+\frac{5π}{12}}]，k∈z$ | D． | $[{kπ+\frac{π}{6}，kπ+\frac{5π}{6}}]，k∈z$ |
13．若实数x，y满足$\left\{\begin{array}{l}{x-y+1＞0}\\{2x-y＜0}\end{array}\right.$，则点P（x，y）不可能落在（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |