题目内容
18.已知点M(3,1),直线ax-y+4=0及圆(x-1)2+(y-2)2=4.(1)若直线ax-y+4=0与圆相切,求a的值.
(2)求过M点的圆的切线方程.
分析 (1)根据圆的切线到圆心的距离等于半径,利用点到直线的距离公式建立关于a的方程,解之即可得到a的值;
(2)根据圆的切线到圆心的距离等于半径,可得当直线的斜率不存在时方程为x=3,符合题意.而直线的斜率存在时,利用点斜式列式并结合点到直线的距离公式加以计算,得到切线方程为3x-4y-5=0,即可得到答案.
解答 解:(1)圆心坐标C(1,2),半径R=2,
若若直线ax-y+4=0与圆C相切,
则圆心到直线的距离d=$\frac{|a+2|}{\sqrt{1+{a}^{2}}}$=2,
解得a=0或a=$\frac{4}{3}$…(4分)
(2)圆心C(1,2),半径为r=2,
当直线的斜率不存在时,直线方程为x=3,
由圆心C(1,2)到直线x=3的距离d=3-1=2=r知,
直线与圆相切.
当直线的斜率存在时,设方程y-1=k(x-3),
即kx-y+1-3k=0,
由题意知$\frac{|k-2+1-3k|}{\sqrt{1+{k}^{2}}}$=2,解得k=$\frac{3}{4}$,
即直线方程为y-1=$\frac{3}{4}$(x-3),
即3x-4y-5=0,
综上所述,过M点的圆的切线方程为x=3或3x-4y-5=0.
点评 本题主要考查直线和圆的位置关系的应用,根据点到直线的距离公式以及相交弦长公式是解决本题的关键.

练习册系列答案
相关题目
10.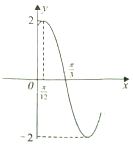 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )
 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图所示,把f(x)的图象向右平移$\frac{π}{3}$个单位长度得到g(x)的图象,则g(x)的单调递增区间是( )| A. | $[{kπ-\frac{5π}{12},kπ+\frac{π}{12}}],k∈z$ | B. | $[{kπ-\frac{π}{6},kπ+\frac{π}{3}}],k∈z$ | ||
| C. | $[{kπ-\frac{π}{12},kπ+\frac{5π}{12}}],k∈z$ | D. | $[{kπ+\frac{π}{6},kπ+\frac{5π}{6}}],k∈z$ |
13.若实数x,y满足$\left\{\begin{array}{l}{x-y+1>0}\\{2x-y<0}\end{array}\right.$,则点P(x,y)不可能落在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
 ,则
,则 的最大值为( )
的最大值为( )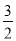 C.1 D.
C.1 D.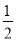

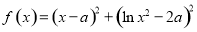 ,其中
,其中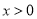 ,
,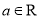 ,存在
,存在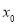 使得
使得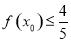 成立,则实数
成立,则实数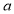 的值为( )
的值为( ) B.
B.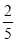 C.
C.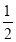 D.
D.