题目内容
13.已知实数u,v满足u>|v|,2u=3(u2-v2),则3u+v的取值范围是[$\frac{3+2\sqrt{2}}{3},+∞$).分析 把已知条件变形,然后作出可行域,在利用线性规划知识求解.
解答 解:由u>|v|,得$\left\{\begin{array}{l}{v≥0}\\{u>v}\end{array}\right.$或$\left\{\begin{array}{l}{v<0}\\{u>-v}\end{array}\right.$;
由2u=3(u2-v2),得$(u-\frac{1}{3})^{2}-{v}^{2}=\frac{1}{3}$.
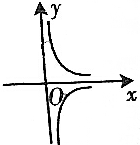
作出可行域如图双曲线右支,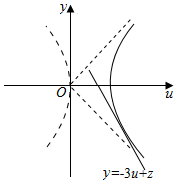
令z=3u+v,化为v=-3u+z,
联立$\left\{\begin{array}{l}{2u=3({u}^{2}-{v}^{2})}\\{v=-3u+z}\end{array}\right.$,消去v得:24u2+(2-18z)u+3z2=0.
由△=(2-18z)2-12×24z2=0,得9z2-18z+1=0.
解得:$z=\frac{3-2\sqrt{2}}{3}$(舍)或$z=\frac{3+2\sqrt{2}}{3}$.
∴3u+v的取值范围是[$\frac{3+2\sqrt{2}}{3},+∞$).
故答案为:[$\frac{3+2\sqrt{2}}{3},+∞$).
点评 本题考查简单的线性规划,考查了数形结合的解题思想方法和数学转化思想方法,属中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
4.某公司为了解用户对其产品的满意度,从某地区随机调查了100个用户,得到用户对产品的满意度评分频率分布表如下:
(1)根据上面的频率分布表,估计该地区用户对产品的满意度评分超过70分的概率;
(2)请由频率分布表中数据计算众数、中位数,平均数,根据样本估计总体的思想,若平均分低于75分,视为不满意.判断该地区用户对产品是否满意?
| 组别 | 分组 | 频数 | 频率 |
| 第一组 | (50,60] | 10 | 0.1 |
| 第二组 | (60,70] | 20 | 0.2 |
| 第三组 | (70,80] | 40 | 0.4 |
| 第四组 | (80,90] | 25 | 0.25 |
| 第五组 | (90,100) | 5 | 0.05 |
| 合计 | 100 | 1 |
(2)请由频率分布表中数据计算众数、中位数,平均数,根据样本估计总体的思想,若平均分低于75分,视为不满意.判断该地区用户对产品是否满意?
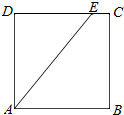 如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.
如图,在边长为2的正方形ABCD中,E为正方形边上的动点,现将△ADE所在平面沿AE折起,使点D在平面ABC上的射影H在直线AE上,当E从点D运动到C,再从C运动到B,则点H所形成轨迹的长度为π.