题目内容
2.利用几何法和定义法计算:${∫}_{-2}^{1}$|x|dx.分析 定义法:(-2,1)区间分为(-2,0)和(0,1)化简被积函数|x|得到积分和求出即可;
几何法:根据定积分几何意义转化为求对应曲线围成的面积即可.
解答 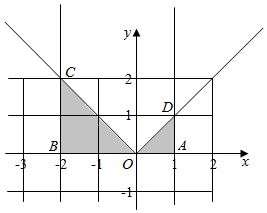 解:定义法:${∫}_{-2}^{1}$|x|dx=${∫}_{-2}^{0}$-xdx+${∫}_{0}^{1}$xdx=-$\frac{1}{2}$x2|${\;}_{-2}^{0}$+$\frac{1}{2}$x2|${\;}_{0}^{1}$=2+$\frac{1}{2}$=$\frac{5}{2}$,
解:定义法:${∫}_{-2}^{1}$|x|dx=${∫}_{-2}^{0}$-xdx+${∫}_{0}^{1}$xdx=-$\frac{1}{2}$x2|${\;}_{-2}^{0}$+$\frac{1}{2}$x2|${\;}_{0}^{1}$=2+$\frac{1}{2}$=$\frac{5}{2}$,
几何法:的几何意义是由曲线y=|x|,直线x=-2,x=1围成的封闭图形的面积,
如图:则A(1,0),B(-2,0),C(-2,-2),D(1,1)
${∫}_{-2}^{1}$|x|dx=S△ADO+S△OBC=$\frac{1}{2}$×1×1+$\frac{1}{2}$×2×2=$\frac{5}{2}$.
点评 本题主要考查定积分的基本运算,解题关键是找出被积函数的原函数,利用区间去绝对值符号也是注意点,本题属于基础题.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
12.一位同学家里订了一份报纸,送报人每天都在在早上5:20~6:40之间将报纸送达,该同学的爸爸需要早上6:00~7:00之间出发去上班,则这位同学的爸爸在离开家前能拿到报纸的概率是( )
| A. | $\frac{3}{9}$ | B. | $\frac{5}{6}$ | C. | $\frac{7}{18}$ | D. | $\frac{1}{2}$ |