题目内容
5.设函数$f(x)=\left\{{\begin{array}{l}{1,x有理数}\\{0,x为无理数}\end{array}}\right.$,则关于函数f(x)有以下四个命题( )①?x∈R,f(f(x))=1;
②?x0,y0∈R,f(x0+y0)=f(x0)+f(y0);
③函数f(x)是偶函数;
④函数f(x)是周期函数.
其中真命题的个数是( )
| A. | 4 | B. | 3 | C. | 2 | D. | 1 |
分析 由函数的值的求法、函数的性质逐一核对四个命题得答案.
解答 解:由$f(x)=\left\{{\begin{array}{l}{1,x有理数}\\{0,x为无理数}\end{array}}\right.$,
可得f(x)=0或1,则?x∈R,f(f(x))=1,故①正确;
当${x}_{0}=\sqrt{2},{y}_{0}=\sqrt{3}$时,f(x0+y0)=f(x0)+f(y0),故②正确;
∵x为有理数,则-x为有理数,x为无理数,则-x为无理数,∴函数f(x)是偶函数,故③正确;
任何一个非0的有理数都是函数的周期,∴函数f(x)是周期函数,故④正确.
∴真命题的个数是4个.
故选:A.
点评 本题考查命题的真假判断与应用,考查函数的性质,是中档题.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
16.已知集合A={x|x2-2x-3<0},B={x|-2<x<2},则A∩B=( )
| A. | {x|-2<x<2} | B. | {x|-2<x<3} | C. | {x|-1<x<3} | D. | {x|-1<x<2} |
20.据统计,截至2016年底全国微信注册用户数量已经突破9.27亿,为调查大学生这个微信用户群体中每人拥有微信群的数量,现从某市大学生中随机抽取100位同学进行了抽样调查,结果如下:
(Ⅰ)求a,b,c的值及样本中微信群个数超过12的概率;
(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过12的概率;
(Ⅲ)以(1)中的频率作为概率,若从全市大学生中随机抽取3人,记X表示抽到的是微信群个数超过12的人数,求X的分布列和数学期望E(X).
| 微信群数量(个) | 频数 | 频率 |
| 0~4 | 0.15 | |
| 5~8 | 40 | 0.4 |
| 9~12 | 25 | |
| 13~16 | a | c |
| 16以上 | 5 | b |
| 合计 | 100 | 1 |
(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过12的概率;
(Ⅲ)以(1)中的频率作为概率,若从全市大学生中随机抽取3人,记X表示抽到的是微信群个数超过12的人数,求X的分布列和数学期望E(X).
17.已知集合A={x|x2-2x-3<0},$B=\{x|\frac{1-x}{x}<0\}$,则A∩B=( )
| A. | {x|1<x<3} | B. | {x|-1<x<3} | C. | {x|-1<x<0或0<x<3} | D. | {x|-1<x<0或1<x<3} |
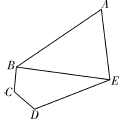 某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$.
某学校的平面示意图为如下图五边形区域ABCDE,其中三角形区域ABE为生活区,四边形区域BCDE为教学区,AB,BC,CD,DE,EA,BE为学校的主要道路(不考虑宽度).$∠BCD=∠CDE=\frac{2π}{3}$,$∠BAE=\frac{π}{3},DE=3BC=3CD=\frac{9}{10}km$.