题目内容
20.据统计,截至2016年底全国微信注册用户数量已经突破9.27亿,为调查大学生这个微信用户群体中每人拥有微信群的数量,现从某市大学生中随机抽取100位同学进行了抽样调查,结果如下:| 微信群数量(个) | 频数 | 频率 |
| 0~4 | 0.15 | |
| 5~8 | 40 | 0.4 |
| 9~12 | 25 | |
| 13~16 | a | c |
| 16以上 | 5 | b |
| 合计 | 100 | 1 |
(Ⅱ)若从这100位同学中随机抽取2人,求这2人中恰有1人微信群个数超过12的概率;
(Ⅲ)以(1)中的频率作为概率,若从全市大学生中随机抽取3人,记X表示抽到的是微信群个数超过12的人数,求X的分布列和数学期望E(X).
分析 (Ⅰ)在0至4这一段,对应的频数为15,由此能求出a,b,c的值及样本中微信群个数超过12的概率.
(Ⅱ)记“2人中恰有1人微信群个数超过12”为事件A,利用等可能事件概率计算公式能求出2人中恰有1人微信群个数超过12的概率.
(Ⅲ)由题意知微信群个数超过12的概率为P=$\frac{1}{5}$,X的所有可能取值为0,1,2,3,分别求出相应的概率,由此能求出X的分布列和E(X).
解答 解:(Ⅰ)在0至4这一段,对应的频数为15,
由已知得:15+40+25+a+5=100,
解得a=15,
∴b=$\frac{5}{100}$=0.05,c=$\frac{15}{100}=0.15$,c=$\frac{15}{100}$=0.15,
样本中微信群个数超过12的概率p=$\frac{20}{100}=\frac{1}{5}$.
(Ⅱ)记“2人中恰有1人微信群个数超过12”为事件A,
则P(A)=$\frac{{C}_{20}^{1}{C}_{40}^{1}}{{C}_{200}^{2}}$=$\frac{32}{99}$,
∴2人中恰有1人微信群个数超过12的概率为$\frac{32}{99}$.
(Ⅲ)由题意知微信群个数超过12的概率为P=$\frac{1}{5}$,
X的所有可能取值为0,1,2,3,
则P(X=0)=${C}_{3}^{0}(1-\frac{1}{5})^{3}$=$\frac{64}{125}$,
P(X=1)=${C}_{3}^{1}(\frac{1}{5})(1-\frac{1}{5})^{2}$=$\frac{48}{125}$,
P(X=2)=${C}_{3}^{2}(\frac{1}{5})^{2}(1-\frac{1}{5})$=$\frac{12}{125}$,
P(X=3)=${C}_{3}^{3}(\frac{1}{5})^{3}$=$\frac{1}{125}$,
∴X的分布列为:
| X | 0 | 1 | 2 | 3 |
| P | $\frac{64}{125}$ | $\frac{48}{125}$ | $\frac{12}{125}$ | $\frac{1}{125}$ |
点评 本题考查概率的求法,考查离散型随机变量的分布列及数学期望的求法,考查推理论证能力、运算求解能力、空间思维能力,考查数形结合思想、转化化归思想,是中档题.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案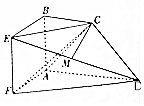 如图,已知四边形ABEF于ABCD分别为正方形和直角梯形,平面ABEF⊥平面ABCD,AB=BC=$\frac{1}{2}$AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.
如图,已知四边形ABEF于ABCD分别为正方形和直角梯形,平面ABEF⊥平面ABCD,AB=BC=$\frac{1}{2}$AD=1,AB⊥AD,BC∥AD,点M是棱ED的中点.