题目内容
实数a,b满足a-
b=1,则4a+2-b的最小值为 .
| 1 |
| 2 |
考点:基本不等式
专题:不等式的解法及应用
分析:利用基本不等式的性质、指数运算法则即可得出.
解答:
解:∵a-
b=1,∴2a-b=2.
∴4a+2-b≥2
=2
=2
=4,当且仅当2a=-b=1时取等号.
∴4a+2-b的最小值为4.
故答案为:4.
| 1 |
| 2 |
∴4a+2-b≥2
| 4a•2-b |
| 22a-b |
| 22 |
∴4a+2-b的最小值为4.
故答案为:4.
点评:本题考查了基本不等式的性质、指数运算法则,属于基础题.

练习册系列答案
相关题目
如图所示空间四边形ABCD,连接AC、BD,设M、G分别是BC、CD的中点,则
-
+
等于( )
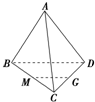
| MG |
| AB |
| AD |

A、
| ||||
B、3
| ||||
C、3
| ||||
D、2
|
已知函数f(x)=
若0<x1<x2<1,则( )
| 1-x2 |
A、
| ||||
B、
| ||||
C、
| ||||
| D、前三个判断都不正确 |
复数z=
(i为虚数单位)的虚部为( )
| 2+i |
| i |
| A、2 | B、-2 | C、1 | D、-1 |
