题目内容
20.给出下列命题:(1)若函数h(x)=cos4x-sin4x,则h′($\frac{π}{2}$)=1;
(2)若函数g(x)=(x-1)(x-2)(x-3)…(x-2015)(x-2016),则g′(2016)=2015!;
(3)若函数f(x)=$\frac{sinx}{2+cosx}$的单调递增区间是(2kπ-$\frac{2π}{3}$,2kπ+$\frac{2π}{3}$)(k∈Z)
(4)若三次函数f(x)=ax3+bx2+cx+d,则“a+b+c=0”是“f(x)有极值点”的充分条件;
其中正确的命题序号为(2)、(3)、(4).
分析 (1)求出函数h(x)的导数,计算h′($\frac{π}{2}$)的值即可判断正误;
(2)求出函数g(x)的导数,计算g′(2016)的值即可;
(3)求函数f(x)的导数,得出f′(x)>0时x的取值范围即可;
(4)判断a+b+c=0时f(x)有极值点即可.
解答 解:对于(1),函数h(x)=cos4x-sin4x,
∴h′(x)=4cos3x•(-sinx)-4sin3x•cosx,
∴h′($\frac{π}{2}$)=-4cos3$\frac{π}{2}$•sin$\frac{π}{2}$-4sin3$\frac{π}{2}$cos$\frac{π}{2}$=0,(1)错误;
对于(2),函数g(x)=(x-1)(x-2)(x-3)…(x-2015)(x-2016),
则g′(x)=(x-2)(x-3)…(x-2015)(x-2016)+(x-1)(x-3)…
(x-2015)(x-2016)+…+(x-1)(x-2)…(x-2015),
∴g′(2016)=1×2×3×…×2015=2015!,(2)正确;
对于(3),函数f(x)=$\frac{sinx}{2+cosx}$,
∴f′(x)=$\frac{cos(2+cosx)-sinx•(-sinx)}{{(2+cosx)}^{2}}$=$\frac{1+2cosx}{{(2+cosx)}^{2}}$,
令f′(x)>0,得cosx>-$\frac{1}{2}$,
解得2kπ-$\frac{2π}{3}$<x<2kπ+$\frac{2π}{3}$,k∈Z;
∴f(x)的单调递增区间是(2kπ-$\frac{2π}{3}$,2kπ+$\frac{2π}{3}$)(k∈Z),(3)正确;
对于(4),三次函数f(x)=ax3+bx2+cx+d,则f′(x)=3ax2+2bx+c,
要使函数f(x)有极值,则△=b2-3ac≥0,
a+b+c=0满足条件,是“f(x)有极值点”的充分条件,(4)正确.
综上,正确的命题序号为(2)、(3)、(4).
故答案为:(2)、(3)、(4).
点评 本题考查了命题真假的判断问题,要求熟练掌握判断命题真假的判断方法和相关知识,是综合性题目.

 举一反三单元同步过关卷系列答案
举一反三单元同步过关卷系列答案| A. | M={(3,2)},N={(2,3)} | B. | M={2,3},N={3,2} | ||
| C. | M={(x,y)|x+y=1},N={y|x+y=1} | D. | M={2,3},N={(2,3)} |
| A. | (0,$\frac{2}{3}$] | B. | [$\frac{2}{3}$,$\frac{3}{4}$] | C. | [$\frac{1}{3}$,$\frac{2}{3}$] | D. | [$\frac{1}{3}$,$\frac{2}{3}$) |
| A. | (-a2b)2•(-ab2)3=-a7b8 | B. | [-(a3)2•(-b2)3]3=a18b18 | ||
| C. | (-a3)2•(-b2)3=a6b6 | D. | (-a2b3)3÷(-ab2)3=a3b3 |
| A. | 4 | B. | 2 | C. | 4+2△x | D. | 4+2(△x)2 |
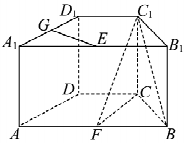 如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.
如图,在直四棱柱ABCD-A1B1C1D1中,底面ABCD为等腰梯形,AB∥CD,AB=4,BC=CD=2,AA1=2,E、F、G分别是棱A1B1、AB、A1D1的中点.