题目内容
12.已知半径为$2\sqrt{3}$的球内有一内接正方体,若在球内任取一点,则该点在正方体内的概率为$\frac{2\sqrt{3}}{3π}$.分析 半径为$2\sqrt{3}$的球的体积为$\frac{4}{3}π•(2\sqrt{3})^{3}$=$32\sqrt{3}π$,正方体的棱长为4,求出正方体的体积,根据几何概型的公式,求出该点落在正方体内的概率即可.
解答 解:半径为$2\sqrt{3}$的球的体积为$\frac{4}{3}π•(2\sqrt{3})^{3}$=$32\sqrt{3}π$,正方体的棱长为4,
所以正方体的体积为:4×4×4=64,
则该点落在正方体内的概率为:$\frac{64}{32\sqrt{3}π}$=$\frac{2\sqrt{3}}{3π}$.
故答案为:$\frac{2\sqrt{3}}{3π}$.
点评 本题主要考查了几何概型的应用,属于基础题,解答此题的关键是根据正方体及其外接球的位置关系,求出正方体的棱长.

练习册系列答案
相关题目
9.不等式组$\left\{\begin{array}{l}-1≤x≤1\\ 0≤y≤2\end{array}\right.$表示的点集M,不等式组$\left\{\begin{array}{l}{x-y+1≥0}\\{y≥2{x}^{2}}\end{array}\right.$表示的点集记为N,在M中任取一点P,则P∈N的概率为( )
| A. | $\frac{5}{32}$ | B. | $\frac{9}{32}$ | C. | $\frac{9}{16}$ | D. | $\frac{5}{16}$ |
7.已知一个几何体的三视图如图所示,则该几何体的体积是( )
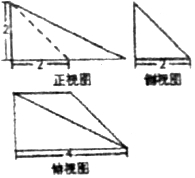

| A. | 2 | B. | 4 | C. | 6 | D. | 1 |