题目内容
若△ABC内接于以O为圆心,1为半径的圆,且
+
+
=
,且|
|=|
|,则
•
=( )
| OA |
| AB |
| OC |
| 0 |
| OA |
| AB |
| CA |
| CB |
| A、3 | ||
B、
| ||
C、
| ||
D、2
|
考点:平面向量数量积的运算
专题:平面向量及应用
分析:如图所示,由
+
+
=
+
=
,可得B,O,C三点共线,即BC是⊙O的直径.由于|
|=|
|,可得|
|=
|
|,因此∠ACB=30°.再利用数量积的定义即可得出.
| OA |
| AB |
| OC |
| OB |
. |
| OC |
| 0 |
| OA |
| AB |
| AB |
| 1 |
| 2 |
| BC |
解答:
解:如图所示,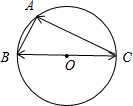
∵
+
+
=
+
=
,
∴B,O,C三点共线,即BC是⊙O的直径.
∴∠BAC=Rt∠.
∵|
|=|
|,
∴|
|=
|
|,
∴∠ACB=30°.
∴|
|=
.
∴
•
=|
||
|cos30°=2×
×
=3.
故选:A.

∵
| OA |
| AB |
| OC |
| OB |
. |
| OC |
| 0 |
∴B,O,C三点共线,即BC是⊙O的直径.
∴∠BAC=Rt∠.
∵|
| OA |
| AB |
∴|
| AB |
| 1 |
| 2 |
| BC |
∴∠ACB=30°.
∴|
| CA |
| 3 |
∴
| CA |
| CB |
| CA |
| CB |
| 3 |
| ||
| 2 |
故选:A.
点评:本题考查了向量的运算、数量积定义、圆的性质、含30°角的直角三角形的性质,考查了计算能力,属于基础题.

练习册系列答案
相关题目
函数f(x)=
+
的定义域是( )
| x-1 |
| 1 |
| x-2 |
| A、[1,+∞) |
| B、(2,+∞) |
| C、(1,2) |
| D、[1,2)∪(2,+∞) |
函数f(x)=
的定义域是( )
| ||
| lgx-1 |
| A、[4,+∞) |
| B、(10,+∞) |
| C、(4,10)∪(10,+∞) |
| D、[4,10)∪(10,+∞) |
若a≠b,数列a,x1,x2,b和数列a,y1,y2,y3,b都是等差数列,则
=( )
| x2-x1 |
| y2-y1 |
A、
| ||
B、
| ||
| C、1 | ||
D、
|
计算:4
=( )
| 3 |
| 2 |
| A、2 | B、6 | C、8 | D、12 |
已知函数f(x)=
,若f(a)=4,则实数a=( )
|
| A、-2或6 | ||
B、-2或
| ||
| C、-2或2 | ||
D、2或
|
阅读如图程序框图,若输出结果为0,则①处的执行框内应填的是( )


| A、x=-1 | ||
| B、b=0 | ||
| C、x=1 | ||
D、a=
|