题目内容
14．数列$\frac{1}{2}，\frac{1}{6}，\frac{1}{12}，\frac{1}{20}，…$的一个通项公式是（ ）| A． | ${a_n}=\frac{1}{n（n-1）}$ | B． | ${a_n}=\frac{1}{2n（2n-1）}$ | C． | ${a_n}=\frac{1}{n}-\frac{1}{n+1}$ | D． | ${a_n}=1-\frac{1}{n}$ |
分析 根据裂项和规律即可得到数列的通项公式
解答 解：数列$\frac{1}{2}，\frac{1}{6}，\frac{1}{12}，\frac{1}{20}，…$的一个通项公式是$\frac{1}{1×2}$，$\frac{1}{2×3}$，$\frac{1}{3×4}$，$\frac{1}{4×5}$，…，即为（1-$\frac{1}{2}$），（$\frac{1}{2}$-$\frac{1}{3}$），（$\frac{1}{3}$-$\frac{1}{4}$），（$\frac{1}{4}$-$\frac{1}{5}$），…，
∴an=$\frac{1}{n}$-$\frac{1}{n+1}$，
故选：C
点评 本题考查数列的通项公式，考查学生分析解决问题的能力，属于基础题．
练习册系列答案
相关题目
4．
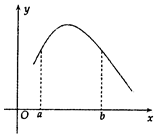函数f（x）的图象如图所示，设f'（x）是f（x）的导函数，若0＜a＜b，下列各式成立的是（ ）
函数f（x）的图象如图所示，设f'（x）是f（x）的导函数，若0＜a＜b，下列各式成立的是（ ）| A． | $f'（{\frac{2ab}{a+b}}）＜f'（{\frac{a+b}{2}}）＜f'（{\sqrt{ab}}）$ | B． | $f'（{\frac{2ab}{a+b}}）＜f'（{\sqrt{ab}}）＜f'（{\frac{a+b}{2}}）$ | ||
| C． | $f'（{\frac{a+b}{2}}）＜f'（{\frac{2ab}{a+b}}）＜f'（{\sqrt{ab}}）$ | D． | $f'（{\frac{a+b}{2}}）＜f'（{\sqrt{ab}}）＜f'（{\frac{2ab}{a+b}}）$ |