题目内容
（本小题满分10分）选修4-5：不等式选讲
已知函数
（Ⅰ）若
.求证：
；
（Ⅱ）若满足
试求实数
的取值范围
（1）根据解析式，直接代入化简变形来证明不等式，体现了作差法的运用。
（2）
解析试题分析：解：（Ⅰ）
..........2分
..........5分
(Ⅱ)由（Ⅰ）可知，
在
为单调增函数.
且
..........7分
当
时，
；
当
时，
；
当
时，
综上所述： ..........10分
考点：函数的单调性，以及绝对值不等式的求解
点评：解决该试题的关键是利用已知函数定义证明单调性，从而求解抽象不等式，属于基础题
练习册系列答案
相关题目
.
满足
，求证：
．
满足
数列
是公差为
，首项
的等差数列； 数列
是公比为
首项
的等比数列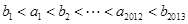，求证：
。
，求证：
的解集为
.
，试比较 
与 
的大小.
的图象；
的不等式
有解，求实数
的取值范围．
为正数，求证：
