已知圆M:(x-1)2+y2=$\frac{3}{8}$.椭圆C:$\frac{{x}^{2}}{3}$+y2=1.若直线l与椭圆交于A.B两点.与圆M相切于点P.且P为AB的中点.则这样的直线l有( )A．2条B．3条C．4条D．6条题目和参考答案——青夏教育精英家教网—

题目内容

20．已知圆M：（x-1）²+y²=$\frac{3}{8}$，椭圆C：$\frac{{x}^{2}}{3}$+y²=1，若直线l与椭圆交于A，B两点，与圆M相切于点P，且P为AB的中点，则这样的直线l有（　　）

A．

2条

B．

3条

C．

4条

D．

6条

分析讨论直线AB的斜率不存在和存在，利用点差法求得直线AB的斜率，根据k_MP•k_AB=-1，求得P点横坐标，确定在椭圆内，即可得到所求直线的条数．

解答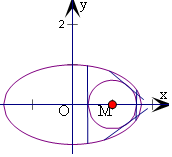解：当直线AB斜率不存在时且与圆M相切时，P在x轴上，
故满足条件的直线有两条；
当直线AB斜率存在时，设A（x₁，y₁），B（x₂，y₂），P（x₀，y₀），
由$\frac{{{x}_{1}}^{2}}{3}$+y₁²=1，$\frac{{{x}_{2}}^{2}}{3}$+y₂²=1，
两式相减，整理得：$\frac{{y}_{1}-{y}_{2}}{{x}_{1}-{x}_{2}}$=-$\frac{1}{3}$•$\frac{{x}_{1}+{x}_{2}}{{y}_{1}+{y}_{2}}$，
则k_AB=-$\frac{{x}_{0}}{3{y}_{0}}$，k_MP=$\frac{{y}_{0}}{{x}_{0}-1}$，k_MP•k_AB=-1，
则k_MP•k_AB=-$\frac{{x}_{0}}{3{y}_{0}}$•$\frac{{y}_{0}}{{x}_{0}-1}$=-1，解得：x₀=$\frac{3}{2}$，
由$\frac{3}{2}$＜$\sqrt{3}$，可得P在椭圆内部，
则这样的P点有两个，即直线AB斜率存在时，也有两条．
综上可得，所求直线l有4条．
故选：C．

点评本题考查点差法的应用，直线的斜率公式、中点坐标公式以及两直线垂直的条件，考查分类讨论和计算能力，属于中档题．

练习册系列答案

11．设m，n是两条不同直线，α，β，γ是三个不同平面，有下列说法：
①若α⊥β，m?β，则m⊥α
②若α∥β，m?α，则m∥β
③若n⊥α，n⊥β，m⊥α，则m⊥β
④若α⊥γ，β⊥γ，m⊥α，则m⊥β
其中正确的是（　　）

8．设数列{a_n}是等差数列，若a₂+a₄+a₆=12，则a₁+a₂+…+a₇等于（　　）

15．已知数列{a_n}的前n项和为S_n，点$（n，\frac{{S}_{n}}{n}）$在直线y=$\frac{1}{2}x+\frac{11}{2}$上，数列{b_n}为等差数列，且b₃=11，前9项和为153．
（1）求数列{a_n}、{b_n}的通项公式；
（2）设c_n=$\frac{3}{（2{a}_{n}-11）（2{b}_{n}-1）}$，数列{c_n}的前n项和为T_n，求使不等式T_n＞$\frac{k}{57}$对一切的n∈N^*都成立的最大整数k．

5．函数y=$\frac{1}{2}sin2x+{sin^2}$x，x∈R的递减区间为（　　）

	A．	$[{kπ-\frac{π}{8}，kπ+\frac{π}{8}}]，k∈Z$		B．	$[{\frac{kπ}{2}-\frac{π}{8}，\frac{kπ}{2}+\frac{π}{8}}]，k∈Z$
	C．	$[{kπ+\frac{3π}{8}，kπ+\frac{7π}{8}}]，k∈Z$		D．	$[{\frac{kπ}{2}+\frac{3π}{8}，\frac{kπ}{2}+\frac{7π}{8}}]，k∈Z$

4．