题目内容

20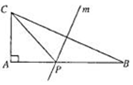．如图，直角三角形ABC（AB＞AC）的斜边BC的垂直平分线m交直角边AB于点P，两条直角边的长度之和为6，设AB=x，求△ACP面积的最大值和相应x的值．

分析 求出PA，AC，可得△ACP面积，利用基本不等式，即可得出结论．

解答 解：AB=x，则AC=6-x，而PB=PC=AB-PA=x-PA，
又PA2+AC2=PA2+（6-x）2=PC2，
联立解得PA=$\frac{6x-18}{x}$，
从而三角形PAC面积S=$\frac{1}{2}$PA•AC=$\frac{（3x-9）（6-x）}{x}$
=27-3（x+$\frac{18}{x}$）≤27-18$\sqrt{2}$
当且仅当最大值点x=3$\sqrt{2}$，从而面积的最大值为27-18$\sqrt{2}$．

点评 本题考查三角形面积的计算，考查基本不等式的运用，属于中档题．

练习册系列答案
相关题目
10．在直角坐标系xOy中，直线l的参数方程为$\left\{\begin{array}{l}x=3+tcosα\\ y=1+tsinα\end{array}\right.$（t为参数），在极坐标系（与直角坐标系xOy取相同的长度单位，且以原点O为极点，以x轴非负半轴为极轴）中，曲线C的方程ρ=4cosθ．
（1）求曲线C的直角坐标系方程；
（2）若点P（3，1），设圆C与直线l交于点A，B，求|PA|+|PB|的最小值．
11．在空间直角坐标系中，点A（1，2，-3）到xOy平面的距离是（　　）
A．1B．2C．3D．$\sqrt{14}$
8．已知等差数列{an}前5项和为35，a5=11，则a4=（　　）
A．9B．10C．12D．13
15．设数列{an}的前n项和为Sn，对任意n∈N*，函数f（x）=x2-Sncosx+2an-n在定义域内有唯一的零点．若不等式$\frac{λ}{n}$≥$\frac{n+1}{{a}_{n}+1}$对任意n∈N*恒成立，则实数λ的最小值是（　　）
A．1B．$\frac{5}{4}$C．$\frac{3}{2}$D．2
5．“a=10“是“直线ax+4y-2=0与2x-5y+b=0互相垂直”的（　　）
A．充要条件B．必要不充分条件
C．充分不必要条件D．既不充分也必要条件
12．已知直线l：$\sqrt{3}$x-y+1=0，方程x2+y2-2mx-2y+m+3=0表示圆．
（Ⅰ）求实数m的取值范围；
（Ⅱ）当m=3时，试判断直线l与该圆公共点的个数．
6．已知集合A={x|y=$\sqrt{x（x-1）}$+$\sqrt{x}$}，集合B={y|y=sinx+$\sqrt{3}$cosx，x∈R}，全集为R，则（∁RA）∩B为（　　）
A．[-2，2）B．[-2，1）C．[-2，0）∪（0，1）D．[-2，0）∪（0，2]
7．已知直线l：x-y+3=0与圆C：（x+1）2+y2=2，则直线l与圆C的位置关系为相切．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网