题目内容
7.已知直线l:x-y+3=0与圆C:(x+1)2+y2=2,则直线l与圆C的位置关系为相切.分析 求得圆心到直线l:x-y+3=0的距离等于半径,可得直线和圆相切.
解答 解:由于圆心(-1,0)到直线l:x-y+3=0的距离为d=$\frac{|-1+3|}{\sqrt{2}}$=$\sqrt{2}$(半径),
故直线和圆相切,
故答案为:相切.
点评 本题主要考查直线和圆的位置关系的判定方法,点到直线的距离公式的应用,属于基础题.

练习册系列答案
相关题目
2.i是虚数单位,复数z=${({\frac{3-i}{1+i}})^2}$,则复数z的共轭复数表示的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
17.命题:“?x>0,x2-x≥0”的否定形式是( )
| A. | ?x≤0,x2-x>0 | B. | ?x>0,x2-x≤0 | C. | ?x≤0,x2-x>0 | D. | ?x>0,x2-x<0 |
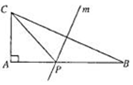 如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.
如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.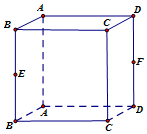 如图,正方体ABCD-A1B1C1D1中,E,F分别是BB1,DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E,F分别是BB1,DD1的中点.