题目内容
12.已知直线l:$\sqrt{3}$x-y+1=0,方程x2+y2-2mx-2y+m+3=0表示圆.(Ⅰ)求实数m的取值范围;
(Ⅱ)当m=3时,试判断直线l与该圆公共点的个数.
分析 (Ⅰ)利用4m2+4-4(m+3)>0,即可求实数m的取值范围;
(Ⅱ)当m=3时,求出圆心到直线的距离大于半径,即可判断直线l与该圆公共点的个数.
解答 解:(Ⅰ)∵方程x2+y2-2mx-2y+m+3=0表示圆,
∴4m2+4-4(m+3)>0⇒m<-1或m>2…(6分)
(Ⅱ)当m=3时,圆的方程可化为(x-3)2+(y-1)2=4
所以圆心为(3,1),半径为r=2…(8分)
圆心到直线的距离$d=\frac{{|{3\sqrt{3}-1+1}|}}{{\sqrt{3+1}}}=\frac{{3\sqrt{3}}}{2}>r$…(10分)
∴直线与圆相离,即直线与圆没有公共点.…(12分)
点评 本题考查圆的方程,考查直线与圆的位置关系,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.若tanα<0,cosα<0,则α的终边所有的象限为( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
7.长方体的长、宽、高分别为2、2、2$\sqrt{2}$,则其外接球的表面积为( )
| A. | 64π | B. | 32π | C. | 16π | D. | 8π |
17.点P是椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上的一点,其左焦点为F(-c,0),若M为线段FP的中点,且M到坐标原点的距离为$\frac{c}{4}$,则$\frac{b}{a}$的取值范围是( )
| A. | (0,$\frac{\sqrt{5}}{3}$) | B. | (0,$\frac{\sqrt{5}}{3}$] | C. | ($\frac{\sqrt{5}}{3}$,1) | D. | [$\frac{\sqrt{5}}{3}$,1) |
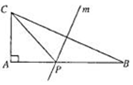 如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.
如图,直角三角形ABC(AB>AC)的斜边BC的垂直平分线m交直角边AB于点P,两条直角边的长度之和为6,设AB=x,求△ACP面积的最大值和相应x的值.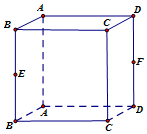 如图,正方体ABCD-A1B1C1D1中,E,F分别是BB1,DD1的中点.
如图,正方体ABCD-A1B1C1D1中,E,F分别是BB1,DD1的中点.