题目内容
已知等比数列{an}中,a1=2,a4=16
(1)求公比q;
(2)若数列{bn}为等差数列,且满足b2=a2-1,b3=
a3,求数列{bn}的通项公式;
(3)求数列{an•bn}的n前项和Tn.
(1)求公比q;
(2)若数列{bn}为等差数列,且满足b2=a2-1,b3=
| 5 |
| 8 |
(3)求数列{an•bn}的n前项和Tn.
考点:数列的求和,等比数列的通项公式,数列递推式
专题:等差数列与等比数列
分析:(1)直接由已知列式求出等比数列的公比;
(2)由(1)求出等比数列的通项公式,得到a2,a3的值,代入b2=a2-1,b3=
a3,求出等差数列{bn}的首项和公差,代入等差数列的通项公式得答案;
(3)把{an}、{bn}代入数列{an•bn},然后直接利用错位相减法求其前n项和Tn.
(2)由(1)求出等比数列的通项公式,得到a2,a3的值,代入b2=a2-1,b3=
| 5 |
| 8 |
(3)把{an}、{bn}代入数列{an•bn},然后直接利用错位相减法求其前n项和Tn.
解答:
解:(1)由
,
∴q3=8,即q=2;
(2)由(1)知an=2n,
∴a2=22=4,a3=23=8.
∴b2=4-1=3,b3=
×8=5.
∴b3-b2=5-3=2.
∴b2-b1=2.
即3-b1=2,解得b1=1.
∴bn=1+2(n-1)=2n-1;
(3)anbn=2n•(2n-1).
∴Tn=1×21+3×22+5×23+…+(2n-3)•2n-1+(2n-1)•2n ①
2Tn=1×22+3×23+5×24+…+(2n-3)•2n+(2n-1)•2n+1 ②
①-②得:-Tn=2+2×22+2×23+…+2×2n-(2n-1)•2n+1
=2+23+24+…+2n+1-(2n-1)•2n+1
=2+
-(2n-1)•2n+1
=2+8(2n-1-1)-(2n-1)-(2n-1)•2n+1
=-(2n-3)•2n+1-6.
Tn=(2n-3)•2n+1+6.
|
∴q3=8,即q=2;
(2)由(1)知an=2n,
∴a2=22=4,a3=23=8.
∴b2=4-1=3,b3=
| 5 |
| 8 |
∴b3-b2=5-3=2.
∴b2-b1=2.
即3-b1=2,解得b1=1.
∴bn=1+2(n-1)=2n-1;
(3)anbn=2n•(2n-1).
∴Tn=1×21+3×22+5×23+…+(2n-3)•2n-1+(2n-1)•2n ①
2Tn=1×22+3×23+5×24+…+(2n-3)•2n+(2n-1)•2n+1 ②
①-②得:-Tn=2+2×22+2×23+…+2×2n-(2n-1)•2n+1
=2+23+24+…+2n+1-(2n-1)•2n+1
=2+
| 8(1-2n-1) |
| 1-2 |
=2+8(2n-1-1)-(2n-1)-(2n-1)•2n+1
=-(2n-3)•2n+1-6.
Tn=(2n-3)•2n+1+6.
点评:本题考查了等比数列的通项公式,考查了错位相减法求数列的和,是中档题.

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
给出函数①y=x3cosx,②y=sin2x,③y=|x2-x|,④y=ex-e-x,其中是奇函数的是( )
| A、①② | B、①④ | C、②④ | D、③④ |
已知两点A(-2,-4),B(1,5)到直线l:ax+y+1=0的距离相等,则实数a的值为( )
| A、-3 | B、3 |
| C、-3或3 | D、1或3 |
若θ∈(
,π),则
的值是( )
| π |
| 2 |
| ||
| sinθ |
| A、1 | B、-1 | C、±1 | D、0 |
已知z=1-i,其中i为虚数单位,则
+z=( )
| 2 |
| z |
| A、2 | B、2+i |
| C、2-i | D、2+2i |
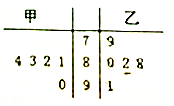 某班甲、乙两位同学升入高中以来的5次数学考试成绩的茎叶图如图,则乙同学这5次数学成绩的中位数是
某班甲、乙两位同学升入高中以来的5次数学考试成绩的茎叶图如图,则乙同学这5次数学成绩的中位数是