题目内容
若θ∈(
,π),则
的值是( )
| π |
| 2 |
| ||
| sinθ |
| A、1 | B、-1 | C、±1 | D、0 |
考点:三角函数的化简求值
专题:三角函数的求值
分析:利用同角三角函数的基本关系式化余弦为正弦,开方后去绝对值得答案.
解答:
解:∵θ∈(
,π),
则
=
=
=
=1.
故选:A.
| π |
| 2 |
则
| ||
| sinθ |
| ||
| sinθ |
| |sinθ| |
| sinθ |
| sinθ |
| sinθ |
故选:A.
点评:本题考查了三角函数的化简与求值,考查了三角函数的象限符号,是基础题.

练习册系列答案
相关题目
 在等腰直角三角形ABC中,AB=AC=1,点P是边AB上异于A、B的一点,光线从点P出发,经BC、CA反射后又回到点P(如图所示),若光线QR经过△ABC的重心,则AP=( )
在等腰直角三角形ABC中,AB=AC=1,点P是边AB上异于A、B的一点,光线从点P出发,经BC、CA反射后又回到点P(如图所示),若光线QR经过△ABC的重心,则AP=( )A、
| ||
B、
| ||
C、
| ||
D、
|
为了得到函数y=cos(2x+1)的图象,只需将函数y=cos2x的图象上所有的点( )
A、向左平移
| ||
B、向右平移
| ||
| C、向左平移1个单位长度 | ||
| D、向右平移1个单位长度 |
下列四条性质:
①最小正周期是π;
②图象关于直线x=
对称;
③图象关于点(
,0)对称;
④在[-
,
]上是增函数.
下列函数同时具有上述性质的一个函数是( )
①最小正周期是π;
②图象关于直线x=
| π |
| 3 |
③图象关于点(
| π |
| 12 |
④在[-
| π |
| 6 |
| π |
| 3 |
下列函数同时具有上述性质的一个函数是( )
A、y=sin(
| ||||
B、y=sin(2x-
| ||||
C、y=cos(2x+
| ||||
D、y=sin(2x+
|
样本数据:2,4,6,8,10的标准差为( )
| A、40 | ||
| B、8 | ||
C、2
| ||
D、2
|
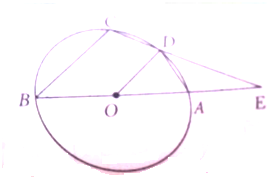 如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.
如图,BA是⊙O的直径,延长BA至E,使得AE=AO,过E点作⊙O的割线交⊙O于D、C,使得AD=DC.