题目内容
9.已知函数f(x)=$\frac{1}{2}$x2-2x-3lnx,g(x)=$\frac{1}{2}$x2-3x-$\frac{1}{2}$a(a∈R).(1)若?x>0,f(x)≥m恒成立,求实数m的取值范围;
(2)设函数F(x)=f(x)-2g(x),若F(x)在[1,5]上有零点,求实数a的取值范围.
分析 (1)?x>0,f(x)≥m恒成立,∴m≤[f(x)]min,利用导数研究其单调性极小值与最小值即可得出.
(2)函数F(x)=f(x)-2g(x)在[1,5]上有零点,等价于方程f(x)-2g(x)=0在[1,5]上有解.化为$\frac{1}{2}{x^2}-4x+3lnx=a$.设$h(x)=\frac{1}{2}{x^2}-4x+3lnx$.利用导数研究其单调性极值与最值,可得函数h(x)在[1,5]上值域即可得出.
解答 解:(1)由题意得f(x)的定义域为(0,+∞),
$f'(x)=x-2-\frac{3}{x}=\frac{{{x^2}-2x-3}}{x}=\frac{(x+1)(x-3)}{x}$.
∵x>0,∴f'(x)、f(x)随x的变化情况如下表:
| x | (0,3) | 3 | (3,+∞) |
| f'(x) | - | 0 | + |
| f(x) | 单调递减 | 极小值 | 单调递增 |
∵f(x)≥m在(0,+∞)上恒成立,∴$m≤-\frac{3}{2}-3ln3$.
(2)函数F(x)=f(x)-2g(x)在[1,5]上有零点,
等价于方程f(x)-2g(x)=0在[1,5]上有解.
化简,得$\frac{1}{2}{x^2}-4x+3lnx=a$.
设$h(x)=\frac{1}{2}{x^2}-4x+3lnx$.
则$h'(x)=x-4+\frac{3}{x}=\frac{(x-1)(x-3)}{x}$,∵x>0,∴h'(x)、h(x)随x的变化情况如下表:
| x | (0,1) | 1 | (1,3) | 3 | (3,+∞) |
| h'(x) | + | 0 | - | 0 | + |
| h(x) | 单调递增 | $-\frac{7}{2}$ | 单调递减 | $3ln3-\frac{15}{2}$ | 单调递增 |
h(5)-h(1)=3ln5-4=ln53-lne4>0.
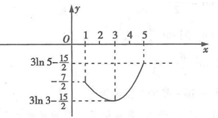
作出h(x)在[1,5]上的大致图象(如图所示).
∴当$3ln3-\frac{15}{2}≤a≤3ln5-\frac{15}{2}$时,
$\frac{1}{2}{x^2}-4x+3lnx=a$在[1,5]上有解.
故实数a的取值范围是$[3ln3-\frac{15}{2},3ln5-\frac{15}{2}]$.
点评 本题考查了利用导数研究函数的单调性极值与最值、等价转化方法、不等式的解法、函数的值域与零点,考查了分析问题与解决问题的能力、数形结合方法、推理能力与计算能力,属于难题.

练习册系列答案
相关题目
19.下面是关于复数z=$\frac{i}{-1+i}$的四个命题,其中的真命题为( )
p1:|z|=$\frac{i}{-1+i}$,p2:z2=2i,p3:z的共轭复数为$\frac{1+i}{2}$,p4:z的虚数为-1.
p1:|z|=$\frac{i}{-1+i}$,p2:z2=2i,p3:z的共轭复数为$\frac{1+i}{2}$,p4:z的虚数为-1.
| A. | p1,p3 | B. | p2,p3 | C. | p2,p4 | D. | p3,p4 |
20.函数y=3sin(-x+$\frac{π}{6}$)的相位和初相分别是( )
| A. | -x+$\frac{π}{6}$,$\frac{π}{6}$ | B. | x+$\frac{5π}{6}$,$\frac{5π}{6}$ | C. | x-$\frac{π}{6}$,-$\frac{π}{6}$ | D. | x+$\frac{5π}{6}$,$\frac{π}{6}$ |