题目内容
18.设复数z=(x-1)+yi(x,y∈R),若|z|≤1,则:(1)复数z对应的点构成的区域的面积为π
(2)y≥x的概率为$\frac{1}{4}-\frac{1}{2π}$.
分析 (1)利用复数的模,求出轨迹方程,利用表达式的几何意义求解面积即可.
(2)判断复数对应点图及内部部分.y≥x的图形是图形中阴影部分,根据几何概率的公式计算即可.
解答 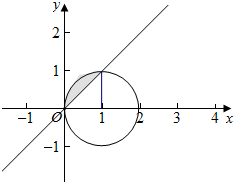 解:(1)复数z=(x-1)+yi(x,y∈R),|z|≤1,
解:(1)复数z=(x-1)+yi(x,y∈R),|z|≤1,
∴(x-1)2+y2≤1,
∴(x,y)在以(1,0)为圆心,以1为半径的圆的上和圆的内部的点,
复数z对应的点构成的区域的面积为:π.
(2)复数对应点图及内部部分,y≥x的图形是图形中阴影部分,
圆的面积为S=π,
S阴影=$\frac{1}{4}$π-$\frac{1}{2}$,
∴则y≥x的概率为P=$\frac{{S}_{阴影}}{S}$=$\frac{\frac{1}{4}π-\frac{1}{2}}{π}$=$\frac{1}{4}-\frac{1}{2π}$,
故答案为:(1)π;(2)$\frac{1}{4}-\frac{1}{2π}$.
点评 本题考查了复数的几何意义,几何概型的概率的求法,关键是求出阴影部分的面积,属于中档题.

练习册系列答案
相关题目
13.已知全集U=Z,集合A={-1,0,1},B={0,1,3},则B∩∁UA=( )
| A. | {3} | B. | {0,1} | C. | {-1} | D. | {-1,3} |