题目内容
6.(1)已知角α终边上一点P(-4,3),求$\frac{{cos(\frac{π}{2}+α)sin(-π-α)}}{{cos(\frac{11π}{2}-α)sin(\frac{9π}{2}+α)}}$的值.(2)设k为整数,化简$\frac{sin(kπ-α)cos[(k+1)π-α]}{sin[(k-1)π+α]cos(kπ+α)}$.
分析 (1)根据点P的坐标求得α的三角函数值,然后利用诱导公式对所求的代数式进行化简,并代入求值即可;
(2)分k为偶数和奇数两种情况,分别利用诱导公式进行化简求值.
解答 解:(1)∵角α终边上一点P(-4,3),
∴x=-4,y=3,r=|OP|=5,sin$α=\frac{y}{r}$=$\frac{3}{5}$,cos$α=\frac{x}{r}$=-$\frac{4}{5}$,
∴$\frac{{cos(\frac{π}{2}+α)sin(-π-α)}}{{cos(\frac{11π}{2}-α)sin(\frac{9π}{2}+α)}}$=$\frac{-sinαsinα}{-sinαcosα}$=$\frac{sinα}{cosα}$=-$\frac{3}{4}$.
(2)当k为偶数时,原式=$\frac{sin(kπ-α)cos[(k+1)π-α]}{sin[(k-1)π+α]cos(kπ+α)}$=$\frac{(-sinα)cosα}{sinαcosα}$=-1;
当k为奇数时,原式=$\frac{sin(kπ-α)cos[(k+1)π-α]}{sin[(k-1)π+α]cos(kπ+α)}$=$\frac{sinα(-cosα)}{(-sinα)(-cosα)}$=-1;
综上可得,$\frac{sin(kπ-α)cos[(k+1)π-α]}{sin[(k-1)π+α]cos(kπ+α)}$=-1.
点评 本题主要考查了诱导公式在三角函数化简求值中的应用,考查了分类讨论思想,属于基础题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
16.已知i是虚数单位,则|$\frac{(-1+i)(1+i)}{{i}^{3}}$|=( )
| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
14.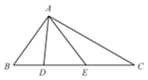 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
 在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )
在△ABC中,D、E是BC边上两点,BD、BA、BC构成以2为公比的等比数列,BD=6,∠AEB=2∠BAD,AE=9,则三角形ADE的面积为( )| A. | 31.2 | B. | 32.4 | C. | 33.6 | D. | 34.8 |
1.已知空间四边形ABCD,满足|$\overrightarrow{AB}$|=3,|$\overrightarrow{BC}$|=7,|$\overrightarrow{CD}$|=11,|$\overrightarrow{DA}$|=9,则$\overrightarrow{AC}$•$\overrightarrow{BD}$的值( )
| A. | -1 | B. | 0 | C. | $\frac{21}{2}$ | D. | $\frac{33}{2}$ |
11.在△ABC中,a,b,c分别是角A,B,C的对边,若a=1,b=$\sqrt{3}$,B=60°,则△ABC的面积为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | 1 | D. | $\sqrt{3}$ |
18.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$$-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)上的一点到双曲线的左、右焦点的距离之差为4,若抛物线y=ax2上的两点A(x1,y1),B(x2,y2)关于直线y=x+m对称,且x1x2=-$\frac{1}{2}$,则m的值为( )
| A. | $\frac{3}{2}$ | B. | $\frac{5}{2}$ | C. | 2 | D. | 3 |
15.已知集合A={x|y=lg(x-1)},B={x|2${\;}^{{x}^{2}-2x}$<1},则A∩B=( )
| A. | {x|x>1} | B. | {x|x>0} | C. | {x|0<x<2} | D. | {x|1<x<2} |
10.已知函数f(x)=2x的值域为A,g(x)=lnx的定义域为B,则( )
| A. | A∩B=(0,1) | B. | A∪B=R | C. | B?A | D. | A=B |