题目内容
16.已知i是虚数单位,则|$\frac{(-1+i)(1+i)}{{i}^{3}}$|=( )| A. | 2 | B. | $\sqrt{3}$ | C. | $\sqrt{2}$ | D. | 1 |
分析 直接利用复数代数形式的乘除运算化简再由复数求模公式计算得答案.
解答 解:$\frac{(-1+i)(1+i)}{{i}^{3}}$=$\frac{-2}{-i}=\frac{-2i}{-{i}^{2}}=-2i$,
则|$\frac{(-1+i)(1+i)}{{i}^{3}}$|=2.
故选:A.
点评 本题考查了复数代数形式的乘除运算,考查了复数模的求法,是基础题.

练习册系列答案
相关题目
4.已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的右焦点为F,过点F作倾斜角为30°的直线与双曲线左右两支各有一个交点,过点F作倾斜角为60°的直线与双曲线右支交于不同的两点,则该双曲线离心率的取值范围是( )
| A. | (1,$\frac{2\sqrt{3}}{3}$) | B. | ($\frac{2\sqrt{3}}{3}$,2) | C. | [$\frac{2\sqrt{3}}{3}$,2] | D. | (2,+∞) |
1.已知f(x)是定义在R上的奇函数,且周期为2,当x∈(0,1]时,f(x)=1-x,则函数f(x)在[0,2017]上的零点个数是( )
| A. | 1008 | B. | 1009 | C. | 2017 | D. | 2018 |
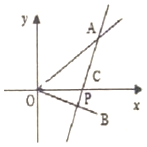 如图,直线OA,OB方程分别为y=x和y=-$\frac{{\sqrt{3}}}{3}$x,过点P(2,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在与直线2x+y+m=0,(m∈R)垂直且过原点的直线上时,求直线AB的方程.
如图,直线OA,OB方程分别为y=x和y=-$\frac{{\sqrt{3}}}{3}$x,过点P(2,0)作直线AB分别交OA,OB于A,B两点,当AB的中点C恰好落在与直线2x+y+m=0,(m∈R)垂直且过原点的直线上时,求直线AB的方程.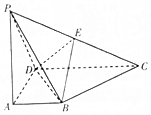 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,PA⊥BC,E是棱PC的中点,∠DAB=90°,AB∥CD,AD=CD=2AB=2.