题目内容
已知双曲线方程是x2－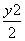
＝1，过定点P(2，1)作直线交双曲线于P1、P2两点，并使P(2，1)为P1P2的中点，则此直线方程是____________．
4x－y－7＝0
练习册系列答案
手拉手全优练考卷系列答案
相关题目
手拉手全优练考卷系列答案题目内容
已知双曲线方程是x2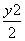－＝1，过定点P(2，1)作直线交双曲线于P1、P2两点，并使P(2，1)为P1P2的中点，则此直线方程是____________．
4x－y－7＝0
手拉手全优练考卷系列答案
，sinα＝
，tan(α－β)＝－
，求cosβ的值．
＝
，那么cosα＝________．
，回答下列问题．
是第几象限的角？
＋
＋y2＝1的左顶点为A，过A作两条互相垂直的弦AM、AN交椭圆于M、N两点．
＝1表示椭圆，则k的取值范围是________.